Пример выполнения работы №3

.

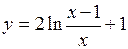Выполним команду restart.

> restart:

Зададим функцию с именем 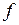и переменной .

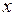> f: =x-> 2*ln((x-1)/x)+1;

Найдём область определения функции. Данная функция определена для всех действительных 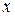, удовлетворяющих неравенству 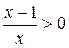. Решая неравенство с помощью функции solve, получаем, что областью определения функции 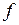является объединение двух интервалов

:

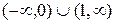> solve((x-1)/x> 0, x);

RealRange(- 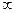, Open(0)), RealRange(Open(1), )

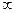Найдем точки разрыва функции

> readlib(discont): discont(f(x), x);

{0, 1}

Точк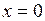и и 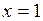являются точками разрыва функции.

Исследуем граничные точки интервалов ООФ 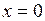и 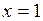с помощью односторонних пределов.

> limit(f(x), x=0, left);

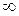
> limit(f(x), x=1, right);

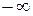
Мы получили, что прямые 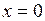и 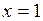являются односторонними вертикальными асимптотами графика исследуемой функции. Этот факт мы учтём при построении графика.

Проверку периодичности функции мы проводить не будем, так как среди элементарных функций периодическими являются только тригонометрические функции, а таковых исследуемая функция не содержит. Далее необходимо проверить функцию на чётность или нечётность.

> simplify(f(-x));

.

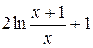Результат показывает, что данная функция не является ни чётной, ни нечётной, так как не выполняется ни одно из условий: 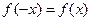− для чётной функции или 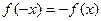− для нечётной. Функция 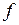− общего вида.

Найдем экстремумы и точки экстремумов с помощью функции extrema. В MapleV для вызова этой функции необходимо предварительно выполнить команду readlib(extrema). Начиная с 7-й версии, этого делать не нужно. Вызов функции осуществляется по правилу extrema(f(x), {}, x, 's'); В переменной с именем s будут храниться координаты точек экстремумов, чтобы их увидеть, нужно вызвать эту переменную.

> readlib(extrema): extrema(f(x), {}, x, 's'); s;

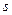
Отклик показал, что функция экстремумов не имеет.

Определим интервалы монотонности функции. Вычислим производную с помощью функции diff и упростим результат с помощью функции simplify.

> d: =simplify(diff(f(x), x));

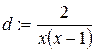
Решим неравенство .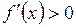

> solve(d> 0, x);

RealRange(- 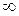, Open(0)), RealRange(Open(1), )

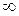Следовательно, на интервалах 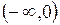, 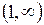функция возрастает.

Найдём точки перегиба, если они есть, и направления выпуклости графика функции. Найдём вторую производную функции как производную от её первой производной.

> d1: =simplify(diff(d, x));

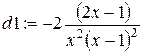
Решим уравнение 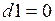с помощью функции solve.

> solve(d1=0, x);

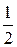
Точка 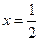не входит в О.О.Ф., следовательно, график функции не имеет точек перегиба.

Решим неравенство .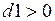

> solve(d1> 0, x);

RealRange(- 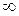, Open(0)), RealRange(Open(0), Open(1/2)).

С учётом области определения делаем вывод, что на интервале 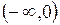график функции направлен выпуклостью вниз. Следовательно, на интервале 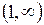график направлен выпуклостью вверх.

Найдем наклонные асимптоты вида 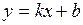с помощью пределов. Вспомним, что , .

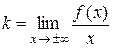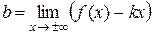> k1: =limit(f(x)/x, x=-infinity);

k1: = 0

> b1: =limit(f(x)-k1*x, x=-infinity);

b1: = 1

> k2: =limit(f(x)/x, x=infinity);

k2: = 0

> b2: =limit(f(x)-k2*x, x=infinity);

b2: = 1

Прямая 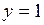является двухсторонней горизонтальной асимптотой, так как .

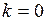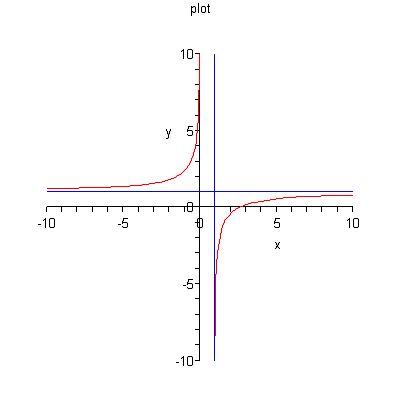
Подтвердим исследование графически. Построим график функции и его асимптоты. Задаём график функции 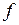и асимптоту 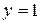с помощью функции plot.

> a: =plot([f(x), 1], x=-10..10, y=-10..10, color=[red, blue], title='plot'):

Вертикальную асимптоту x=1 задаём с помощью функции implicitplot (строит график линии, заданной уравнением 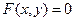) из пакета расширения plots:

> with(plots):

> b: =implicitplot(x=1, x=-10..10, y=-10..10, color=blue):

С помощью функции display из пакета расширения plots выводим изображение на экран на одном рисунке.

> display([a, b]);

Контрольные вопросы

1. Сформулируйте определение понятия функции. Что называется областью определения функции?

2. Какие способы задания функциональной зависимости Вы знаете?

3. Дайте определение непрерывной функции в точке и на некотором числовом множестве.

4. Что такое точка разрыва функции? Приведите классификацию точек разрыва.

5. Какие функции называются элементарными? Приведите примеры.

6. Какая функция называется невозрастающей, неубывающей, возрастающей, убывающей, монотонной?

7. Какой признак монотонности функции Вы знаете?

8. Что называется экстремумом функции? Сформулируйте необходимое, достаточное условия существования экстремума функции.

9. Какая функция называется четной, нечетной, периодической?

10. Что такое промежутки выпуклости и точки перегиба графика функции? Каким образом они находятся?

11. Что называется наклонной и вертикальной асимптотами графика функции?

12. Как находят вертикальные и наклонные асимптоты?

13. Имеет ли непрерывная функция на всей числовой прямой вертикальные асимптоты?