Пример выполнения работы № 5

1. Вычислить повторные интегралы:

а) 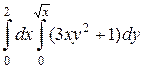; б) .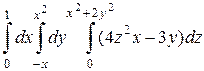

2. Вычислить кратные интегралы:

а) 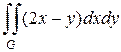, где область 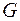ограничена линиями ;

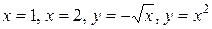б) 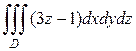, где область 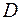ограничена поверхностями

.

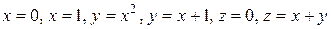1. а) Введем повторный интеграл из условия задачи и вычислим его

> I nt(Int(3*x*y^2+1, y=0..sqrt(x)), x=0..2)= int(int(3*x*y^2+1, y=0..sqrt(x)), x=0..2);

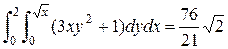
б) Введем повторный интеграл и вычислим его

> Int(Int(Int(4*z^2*x-3*y, z=0..x^2+2*y^2), y=-x..x^2), x=0..1)= int(int(int(4*z^2*x-3*y, z=0..x^2+2*y^2), y=-x..x^2), x=0..1);

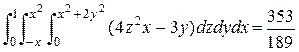
2. а) Область интегрирования представляет собой множество 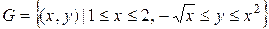. Построим область .

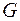> m: =plot([-sqrt(x), x^2], x=1..2, color=[red, red]):

> with(plots):

> k: =implicitplot(x=1, x=1..2, y=-1..1, color=red):

> k1: =implicitplot(x=2, x=1..2, y=-sqrt(2)..4, color=red):

> display([m, k, k1]);

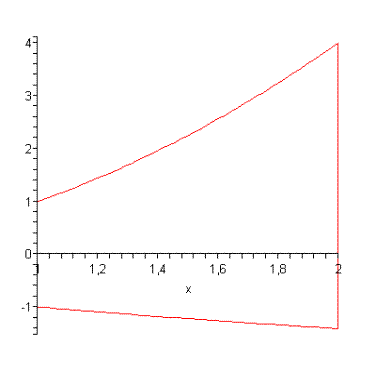
Вычислим двойной интеграл как повторный .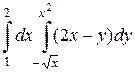

> Int(Int(2*x-y, y=-sqrt(x)..x^2), x=1..2)= int(int(2*x-y, y=-sqrt(x)..x^2), x=1..2);

=

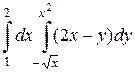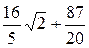
б) Область интегрирования можно задать системой неравенств:

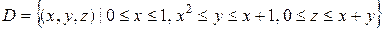. Построим проекцию области 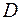на плоскость .

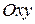> m: =plot([x+1, x^2], x=0..1, color=[red, red]):

> k: =implicitplot(x=0, x=0..1, y=0..1, color=red):

> k1: =implicitplot(x=1, x=0..1, y=1..2, color=red):

> display([m, k, k1]);

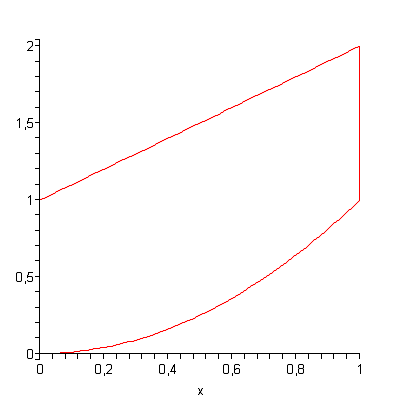
Тогда тройной интеграл сводится к повторному .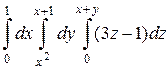

> Int(Int(Int(3*z-1, z=0..x+y), y=x^2..x+1), x=0..1)= int(int(int(3*z-1, z=0..x+y), y=x^2..x+1), x=0..1);

=

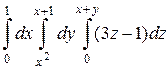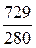
Контрольные вопросы

1. Сформулируйте определение двойного интеграла.

2. В чем состоит геометрический смысл двойного интеграла?

3. Какими свойствами обладает двойной интеграл?

4. Сформулируйте теорему о сведении двойного интеграла к повторному.

5. Что представляет собой определитель Якоби? Как производится замена переменных в двойном интеграле?

6. Как производится вычисление двойного интеграла в полярных координатах?

7. Сформулируйте определение тройного интеграла.

8. В чем состоит геометрический смысл тройного интеграла?

9. Сформулируйте теорему о сведении тройного интеграла к повторному.

10. Как производится вычисление тройного интеграла в цилиндрических и сферических координатах?

ПРИЛОЖЕНИЕ