Екстремальна властивість центра ваги

Для точок 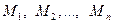на площині їх центром ваги будемо називати таку точку 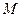, що .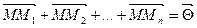

Така точка існує і єдина. Справді, для довільної точки 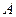з рівності

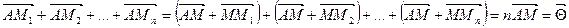
випливає, що точки 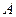та 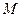співпадають. Відмітимо, що центром ваги для трьох вершин трикутника буде точка перетину його медіан.

Описане геометричне означення узгоджується з фізичним, якщо в точках 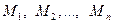розмістити маси однакової величини.

Центр ваги має наступну екстремальну властивість. Для будь-якої точки 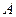виконується нерівність

.

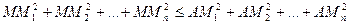Справді, використовуючи скалярний добуток, отримуємо

.

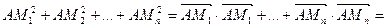
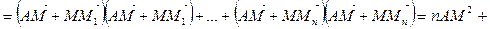
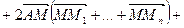
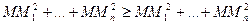Задача 5.4.1. Довести нерівність 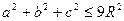, де 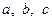- сторони довільного трикутника, 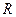- радіус описаного навколо нього кола.

Розв’язання. Нехай 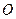- центр описаного кола, 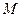- точка перетину медіан 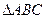. Тоді згідно з доведеним

,

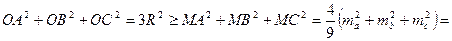
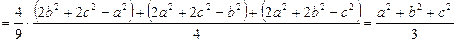що доводить задану нерівність.