Задача 5.3.4. Показати, що в довільному опуклому чотирикутнику відношення найменшої з відстаней між його вершинами до найбільшої з них не перевищує .

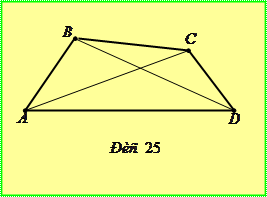
Розв’язання. Нехай М – найбільша, а m – найменша з відстаней між вершинами чотирикутника. В опуклому чотирикутнику хоча б один із кутів не є гострим. На рисунку 25 таким є, наприклад, кут ABС. Використаємо теорему косинусів:

.

Оскільки 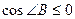, то

.

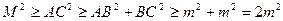Звідси випливає, що 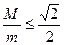. Знак рівності виконується, наприклад, для квадрата.

Задача 5.3.5. Довести, що правильний -кутник має найбільшу площу серед усіх вписаних в коло -кутників.

Розв’язання. Нехай -кутник 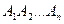вписаний у коло з центром у точці 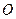та радіусом 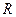. Позначимо 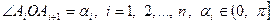. Тоді 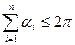(знак строгої нерівності буде у випадку, коли центр кола лежить поза многокутником). Для площі многокутника 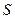маємо 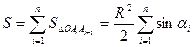. Функція на вказаній множині значень опукла вгору. З нерівності Єнсена отримуємо, що

,

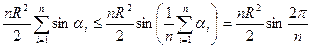а саме останньому значенню дорівнює площа правильного вписаного в коло многокутника.

Задача 5.3.6. В квадраті з стороною 15 розміщено довільним чином 20 квадратиків з стороною 1. Довести, що в квадраті можна додатково розмістити коло з радіусом 1, яке не матиме спільних точок з цими квадратиками.

Розв’язання. Будемо шукати положення для центра кола. Центр має знаходитися на відстані не меншій від 1 від сторін заданого квадрата, тобто всередині квадрата з стороною 13, а також від сторін квадратиків. Для кожного квадратика множина точок, що знаходяться від нього на відстані, меншій від 1, складається з точок самого квадратика, чотирьох квадратиків, побудованих на його сторонах, а також точок чотирьох чвертей кругів з центрами у вершинах квадратика та радіусом 1. Площа фігури, утвореної такими точками, дорівнює 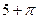. Оскільки сума всіх цих площ дорівнює 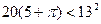, то в квадраті 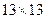знайдеться точка, що не входить до жодної з перерахованих множин. Вона може бути вибрана за центр шуканого кола.

Задача 5.3.7. Дано трикутник і точку 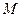всередині нього. Нехай 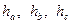- висоти трикутника, проведені до відповідних сторін, 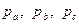- відстані до цих сторін від точки 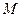. Довести, що

.

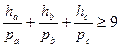Розв’язання. Маємо

.

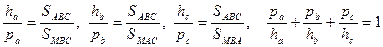Використавши нерівність Коші, отримуємо

.
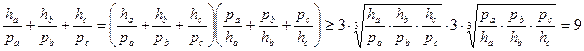