
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Використання співвідношень між елементами геометричних фігур
|
|
В окремих випадках при доведенні нерівностей можна використовувати певні відомі співвідношення між геометричними фігурами. Мова іде про те, що додатним значенням змінних, що фігурують у нерівності присвоюються деякі кількісні характеристики геометричних фігур (довжини відрізків, площі, об’єми), після чого чисто геометричними методами встановлюються необхідні співвідношення: спочатку між геометричними величинами, а потім роблять відповідні висновки про саму алгебраїчну нерівність.
Задача 4.2.1. Довести, що при довільних додатних чисел 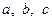 виконується нерівність
виконується нерівність
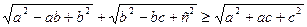 .
.
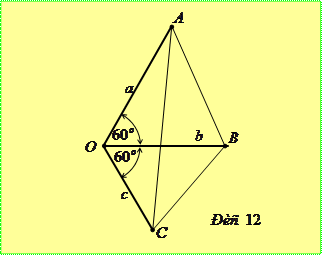
Доведення. Розглянемо відрізки 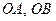 і
і 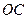 такі, що
такі, що 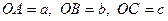 і
і 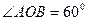 ,
, 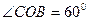 (рис. 12). Маємо
(рис. 12). Маємо 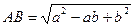 ,
, 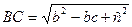 ,
, 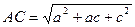 і оскільки
і оскільки 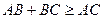 , то нерівність доведено.
, то нерівність доведено.
Задача 4.2.2. При яких значеннях параметра 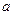 відстань між коренями рівняння
відстань між коренями рівняння
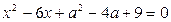
приймає найбільше значення?
 Розв’язання. Перепишемо задане в умові рівняння у виді
Розв’язання. Перепишемо задане в умові рівняння у виді 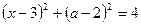 та побудуємо графік одержаної залежності у системі координат
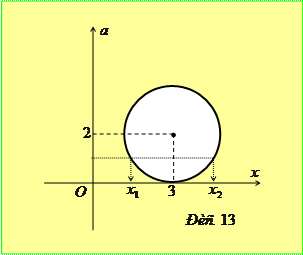
та побудуємо графік одержаної залежності у системі координат 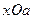 (рис. 13). Очевидно, що при перетині кола прямою
(рис. 13). Очевидно, що при перетині кола прямою 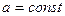 коренями рівняння будуть абсциси точок перетину. Очевидно, що найбільша відстань між коренями рівняння буде дорівнювати діаметру кола, тобто 2 при
коренями рівняння будуть абсциси точок перетину. Очевидно, що найбільша відстань між коренями рівняння буде дорівнювати діаметру кола, тобто 2 при 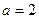 .
.
Задача 4.2.3. Знайти найменше значення виразу
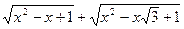 .
.
Розв’язання. Введемо в розгляд функцію
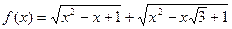 .
.
Насамперед зауважимо, що для всіх 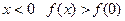 . Тепер зрозуміло, що точку, в якій функція досягає свого найменшого значення, потрібно шукати серед невід’ємних значень змінної.
. Тепер зрозуміло, що точку, в якій функція досягає свого найменшого значення, потрібно шукати серед невід’ємних значень змінної.
Розглянемо випадок, коли 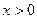 . Тоді можлива наступна геометрична конструкція. Відкладемо два перпендикулярних відрізки
. Тоді можлива наступна геометрична конструкція. Відкладемо два перпендикулярних відрізки 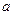 та
та 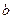 , а також відрізок
, а також відрізок 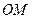 так, що
так, що 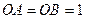 ,
, 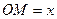 ,
, 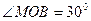 ,
, 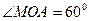 (рис. 14). За теоремою косинусів із трикутників
(рис. 14). За теоремою косинусів із трикутників 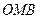 та
та 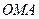 отримуємо
отримуємо
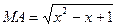 ,
, 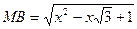 .
.
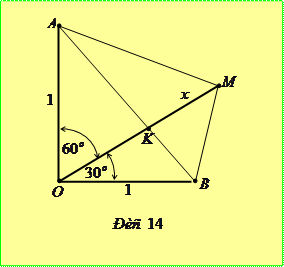 Крім цього бачимо, що
Крім цього бачимо, що 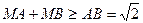 . Рівність досягається тільки у тому випадку, коли точка
. Рівність досягається тільки у тому випадку, коли точка 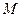 співпадає з точкою
співпадає з точкою 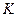 , в якій перетинаються відрізок
, в якій перетинаються відрізок 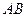 та промінь
та промінь 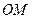 , тобто при
, тобто при 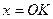 . Довжину відрізка
. Довжину відрізка  знайдемо із
знайдемо із 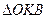 з стороною
з стороною 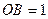 та кутами
та кутами 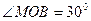 та
та 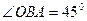 . За теоремою синусів маємо
. За теоремою синусів маємо
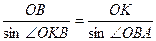 або
або 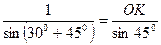 ,
,
звідки 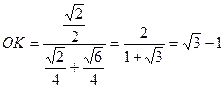 .
.
У випадку 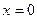 отримуємо
отримуємо 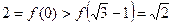 .
.
Отже, найменше значення виразу дорівнює 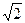 .
.
Задача 4.2.4. Довести нерівність 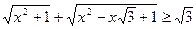 .
.
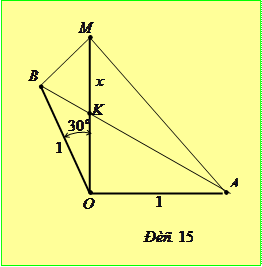 Доведення. Спочатку розглянемо випадок, коли
Доведення. Спочатку розглянемо випадок, коли 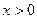 . Тут можлива наступна геометрична конструкція. Відкладемо відрізки
. Тут можлива наступна геометрична конструкція. Відкладемо відрізки 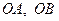 та відрізок
та відрізок 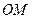 так, що
так, що 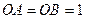 ,
, 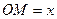 ,
, 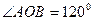 ,
,  та
та 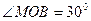 (рис. 15). Тоді
(рис. 15). Тоді 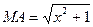 ,
, 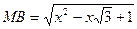 . Тому
. Тому
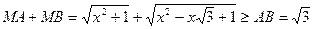 .
.
У випадку, коли 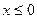 , позначимо
, позначимо 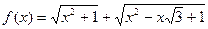 . Тоді для всіх
. Тоді для всіх 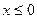 маємо
маємо 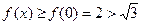 . Тепер можна зробити висновок про те, що задана нерівність виконується при довільних значеннях
. Тепер можна зробити висновок про те, що задана нерівність виконується при довільних значеннях 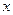 .
.
Задача 4.2.5. Довести, що для довільних значень змінних 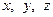 виконується нерівність
виконується нерівність
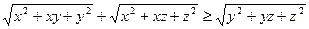 .
.
Доведення. Спочатку розглянемо випадок, коли 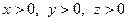 . Відкладемо відрізки
. Відкладемо відрізки 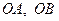 та
та 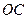 під кутом
під кутом 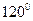 так, щоб
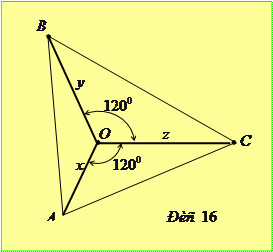
так, щоб 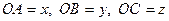 (рис. 16). Зауваживши, що
(рис. 16). Зауваживши, що
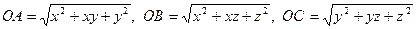
з нерівності трикутника робимо висновок, що задане співвідношення вірне.
Ще дві аналогічні до заданої нерівності отримаємо, зробивши у ній циклічну перестановку змінних 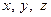 . Мова іде про нерівності
. Мова іде про нерівності
 ,
,
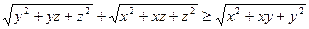 .
.
Розглянемо випадок, коли дві змінні приймають від’ємні, а третя додатне значення (наприклад, 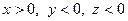 ). Перепозначивши
). Перепозначивши 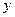 на
на 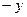 та
та  на
на 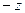 , отримаємо доведену у прикладі 4.2.1 нерівність.
, отримаємо доведену у прикладі 4.2.1 нерівність.
 Якщо дві змінні приймають додатні значення, а третя від’ємні (наприклад,
Якщо дві змінні приймають додатні значення, а третя від’ємні (наприклад, 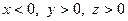 ), то нерівністю у прикладі 4.2.1 можна скористатися, перепозначивши
), то нерівністю у прикладі 4.2.1 можна скористатися, перепозначивши 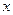 на
на 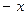 .
.
Випадок, коли всі три змінні приймають від’ємні значення зводиться до початкового доведення шляхом перепозначення 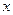 на
на 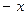 ,
, 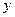 на
на 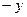 та
та  на
на 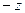 .
.
Доведення нерівності, коли одна, дві або всі три змінні приймають значення 0, очевидні.
Інше доведення даної нерівності, яке використовує ідеї координатного методу, нами було наведено у попередньому розділі (задача 3.1.2).
Задача 4.2.6. Довести нерівність
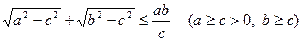 .
.
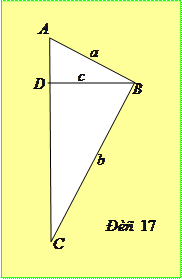 Доведення. При
Доведення. При 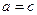 або
або 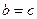 нерівність очевидна. Розглянемо випадок, коли
нерівність очевидна. Розглянемо випадок, коли 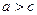 і
і 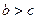 . Перепишемо нерівність у виді
. Перепишемо нерівність у виді 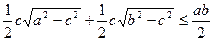 та побудуємо два прямокутні трикутники з спільним катетом
та побудуємо два прямокутні трикутники з спільним катетом 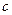 , гіпотенузи яких дорівнюють
, гіпотенузи яких дорівнюють 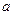 та
та 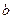 (рис. 17). Тепер ліва частина перетвореної нерівності визначатиме суму площ трикутників
(рис. 17). Тепер ліва частина перетвореної нерівності визначатиме суму площ трикутників 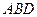 і
і 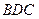 , тобто площу
, тобто площу 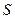 трикутника
трикутника  . Оскільки
. Оскільки 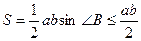 , то нерівність доведена.
, то нерівність доведена.
Задача 4.2.7. Довести, що 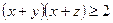 , якщо
, якщо 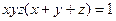 і
і 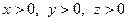 .
.
Доведення. Очевидно, що при 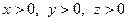 існує трикутник
існує трикутник  такий, що
такий, що 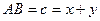 ,
, 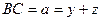 ,
, 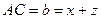 (рис. 18). Нехай точки
(рис. 18). Нехай точки 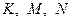 - точки дотику вписаного кола із сторонами
- точки дотику вписаного кола із сторонами 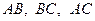 відповідно. Маємо
відповідно. Маємо 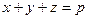 , де
, де 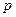 - півпериметр трикутника. Крім того,
- півпериметр трикутника. Крім того,
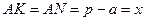 ,
, 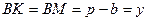 ,
, 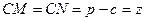 .
.
Але за умовою задачі 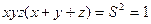 , звідки
, звідки 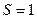 . (
. (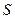 - площа трикутника
- площа трикутника  ). З іншого боку,
). З іншого боку, 
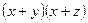 . Тоді
. Тоді 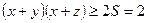 .
.
Задача 4.2.8. Довести нерівність
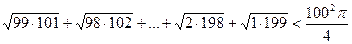 .
.
Доведення. Розглянемо четвертину круга з радіусом 100. Впишемо у нього ступінчату фігуру, яка складається з 99 прямокутників з нижньою основою, що дорівнює 1 (рис. 19). Площа першого прямокутника дорівнює
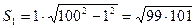 .
.
Для другого прямокутника маємо
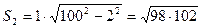 , …,
, …,
 .
.
Площа ступінчатої фігури менша від площі чверті круга, тому
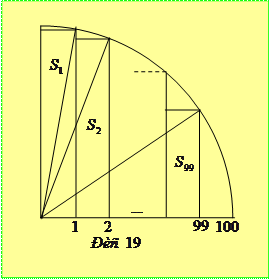

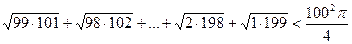 .
.
Розділ 5. Нерівності в геометрії
Геометричні фігури крім притаманних їм чисто геометричних властивостей, описуються також своїми кількісними характеристиками, зокрема довжинами відрізків, величинами кутів, площами, об’ємами, тощо. У практичній діяльності такі величини часто доводиться порівнювати, оцінювати ті межі, в яких вони змінюються (тобто аналізувати числові величини, які вони не можуть перевищувати, або не бути меншими). У результаті виникає ряд геометричних задач, пов’язаних із необхідністю оцінки геометричних величин та доведенням нерівностей, що появляються при цьому.
Окремі міркування, що стосуються певної класифікації методів доведення таких нерівностей, ми розглянемо у вигляді наступних задач.