
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Застосування тригонометрії
|
|
При перетворенні виразів з метою їхнього спрощення іноді використовуються тригонометричні заміни. Такими можуть бути:
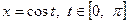 або
або 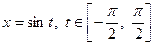 при наявності в умові виразу
при наявності в умові виразу 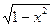 ;
;
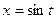 або
або 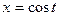 , якщо в умові фігурують блоки
, якщо в умові фігурують блоки 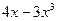 або
або  з перспективою виконати заміни відповідно
з перспективою виконати заміни відповідно 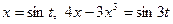 або
або 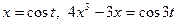 ;
;
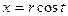 ,
, 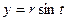 , якщо наявний вираз
, якщо наявний вираз 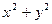 ;
;
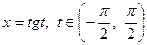 при наявності виразу
при наявності виразу 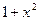 ;
;
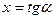 ,
, 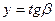 ,
, 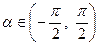 ,
, 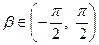 , якщо потрібно перетворювати вираз
, якщо потрібно перетворювати вираз 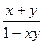 ;
;
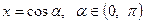 при наявності виразів
при наявності виразів 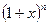 та
та 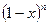 .
.
Наведемо приклади задач, в яких використовуються подібні ідеї.
Задача 3.3.1. Числа 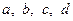 задовольняють умови
задовольняють умови  ,
, 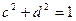 . Довести, що
. Довести, що 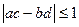 .
.
Доведення. Оскільки  ,
, 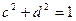 , то існують такі числа
, то існують такі числа 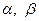 , що
, що 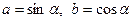 ,
, 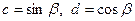 . Отримуємо
. Отримуємо
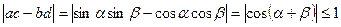 .
.
Задача 3.3.2. Довести, що при 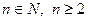 і
і 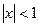 виконується нерівність
виконується нерівність
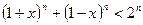 .
.
Доведення. Враховуючи те, що 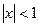 , можна ввести заміну
, можна ввести заміну 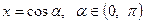 . Тоді
. Тоді
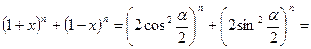
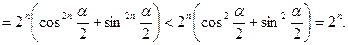
Задача 3.3.3. Дійсні числа 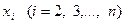 належать відрізку
належать відрізку 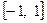 , причому сума кубів цих чисел дорівнює 0. Довести, що
, причому сума кубів цих чисел дорівнює 0. Довести, що 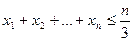 .
.
Доведення. Нехай 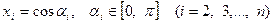 . Маємо
. Маємо
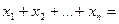
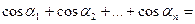
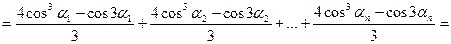
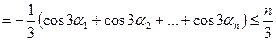 .
.
Задача 3.3.4. Довести, що при довільних дійсних числах  виконується нерівність
виконується нерівність
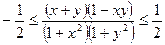 .
.
Доведення. Враховуючи довільність у виборі чисел  , виконаємо заміни
, виконаємо заміни 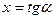 ,
, 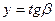 ,
, 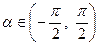 ,
, 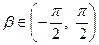 . Тоді
. Тоді
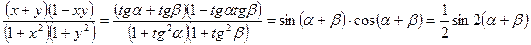 .
.
Звідси випливає справедливість твердження, яке ми доводимо.
Задача 3.3.5. Для довільних дійсних чисел  (крім випадку, коли
(крім випадку, коли 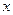 та
та 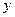 одночасно дорівнюють 0) довести нерівність
одночасно дорівнюють 0) довести нерівність
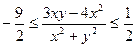 .
.
Доведення. Перейдемо до полярних координат, ввівши заміну 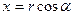 ,
,  (
( ). Дістаємо
). Дістаємо
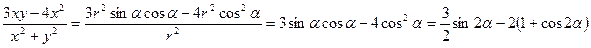 .
.
Тепер оцінимо значення виразу 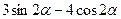 . Маємо
. Маємо
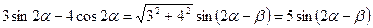 , де
, де 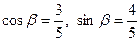 .
.
Таким чином, вираз 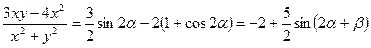 може змінюватися у межах від
може змінюватися у межах від 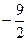 до
до 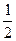 , що доводить задану нерівність.
, що доводить задану нерівність.
Задача 3.3.6. Довести, що із довільних 13 чисел завжди можна вибрати два числа 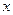 та
та 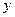 , для яких виконуватиметься нерівність
, для яких виконуватиметься нерівність 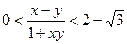 .
.
Доведення. Позначимо через 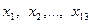 числа, про які іде мова в умові задачі. Нехай
числа, про які іде мова в умові задачі. Нехай 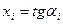 , де
, де 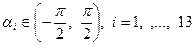 . Розіб’ємо проміжок
. Розіб’ємо проміжок 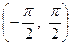 на 12 рівних частин. Тоді знайдуться принаймні два кути
на 12 рівних частин. Тоді знайдуться принаймні два кути 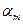 та
та  такі, що
такі, що 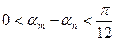 . Звідси
. Звідси 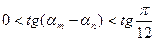 . Нехай
. Нехай 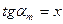 ,
, 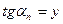 . Тоді
. Тоді 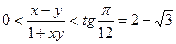 . Доведення рівності
. Доведення рівності 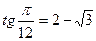 не викликає затруднень. Маємо
не викликає затруднень. Маємо 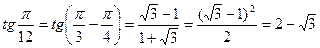 .
.