Застосування методів аналітичної геометрії

Традиційними для аналітичної геометрії є застосування ідеї координатного методу. Відповідно до нього вводиться певна система координат. Після цього кожній парі значень змінних 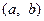можна поставити у відповідність точку з такими ж координатами, лінійному рівнянню відповідатиме на координатній площині пряма. Алгебраїчний вираз 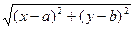тепер можна трактувати, як відстань між двома точками з координатами 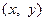та .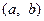

Взагалі кажучи, певні алгебраїчні співвідношення тепер можна розглядати з точки зору співвідношень між геометричними фігурами та величинами. При доведенні нерівностей це робить його геометрично наглядним та створює ширші можливості для пошуку нових ідей доведень. Наведемо приклади.

Задача 3.1.1. Знайти найменше значення виразу

.

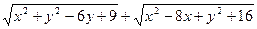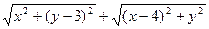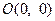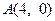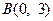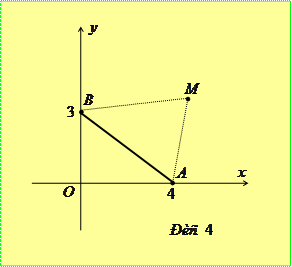
Розв’язання. Запишемо даний вираз у виді та введемо в розгляд точки , , , 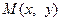(рис. 4). Маємо

,

, .

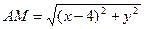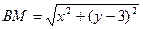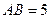Тепер, користуючись нерівністю трикутника, можна стверджувати, що 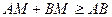і для довільних значень 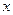та 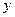виконується співвідношення

.

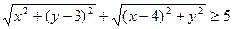Отже, найменше значення виразу дорівнює 5. Рівність буде виконуватися для всіх точок відрізка .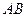

Задача 3.1.2. Довести, що для довільних значень змінних 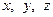виконується нерівність .

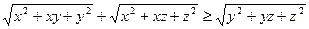Доведення. Розглянемо на координатній площині точки 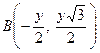, , 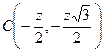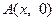. Використавши формулу відстані між двома точками, отримуємо 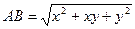, , 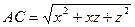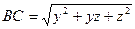. Посилання на нерівність трикутника завершує доведення. Знак рівності виконується, наприклад, при .

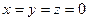Задача 3.1.3. Знайти найбільше та найменше значення виразу 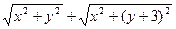, якщо .

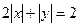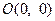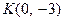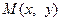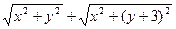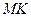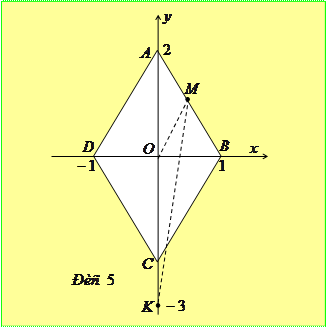
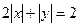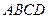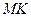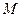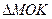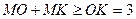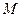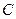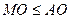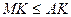Розв’язання. Введемо в розгляд точки , та . Тоді вираз можна трактувати, як суму відрізків та . Графіком залежності є ромб (рис. 5). Умову задачі на мові геометрії тепер можна сформулювати наступним чином: знайти найбільше та найменше значення суми відрізків та , якщо точка належить ромбу. Розглянемо . Маємо (рівність досягається, коли точка співпадає з точкою ). Оскільки і , то 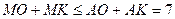(рівність досягається, коли точка 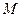співпадає з точкою ).

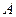Таким чином, найбільше значення виразу буде 7, а найменше значення 3.

Задача 3.1.4. Знайти найменше значення виразу 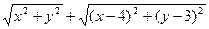, якщо .

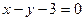Розв’язання. На координатній площині розглянемо точки 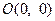, 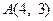і точку 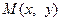, що належить прямій 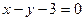. Задача полягає в тому, щоб на вказаній прямій знайти таке положення точки 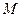, при якому сума відрізків 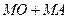буде мінімальною. Нехай точка 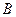симетрична точці 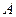відносно прямої 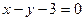. Тоді точка 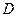, в якій перетнуться прямі 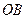та пряма 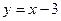, буде шуканою (рис. 6).

Справді, у цьому випадку 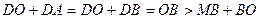для довільної відмінної від 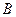точки 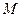. Таким чином, знаходимо точку 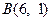та довжину відрізка .

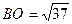Отже, найменше значення виразу 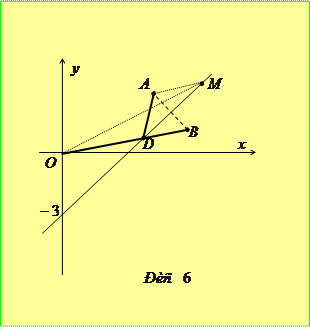буде .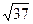

Задача 3.1.5. Довести нерівність

.

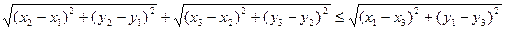Розв’язання. Для доведення достатньо ввести в розгляд точки 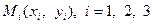, та, зауваживши, що

, ,

,

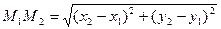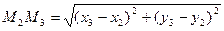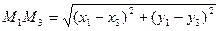скористатися нерівністю трикутника.

Аналогічно до попередньої вправи доводиться нерівність

.
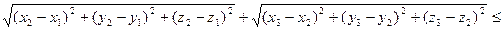
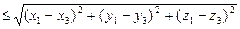