
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оцінка площі
|
|
Нам відомо, що площа трикутника не перевищує половини добутку довільних двох його сторін, а площа опуклого чотирикутника - половини добутку його діагоналей. Ці факти ефективно можна використовувати при розв’язуванні окремих задач. Наведемо приклади.
 Задача 5.3.1. Нехай
Задача 5.3.1. Нехай 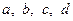 - довжини сторін опуклого чотирикутника. Довести, що його площа не перевищує
- довжини сторін опуклого чотирикутника. Довести, що його площа не перевищує 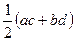 .
.
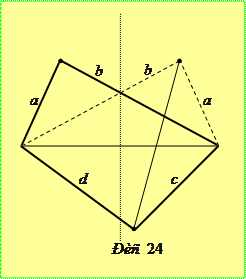
Розв’язання. Проведемо діагональ чотирикутника так, щоб по одну сторону від неї були сторони з довжинами 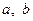 . Симетризуємо ці сторони відносно серединного перпендикуляра до проведеної діагоналі (рис. 24). Утвориться новий чотирикутник тієї ж площі, що заданий, та з довжинами послідовних сторін
. Симетризуємо ці сторони відносно серединного перпендикуляра до проведеної діагоналі (рис. 24). Утвориться новий чотирикутник тієї ж площі, що заданий, та з довжинами послідовних сторін 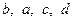 . Провівши у ньому другу діагональ, отримаємо два трикутники, площі яких не перевищують
. Провівши у ньому другу діагональ, отримаємо два трикутники, площі яких не перевищують 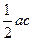 та
та 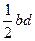 .
.
Задача 5.3.2. Периметр опуклого чотирикутника дорівнює 4. Довести, що його площа не перевищує 1.
Розв’язання. Позначимо сторони чотирикутника через 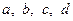 , а його площу через
, а його площу через 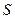 . Тоді
. Тоді 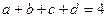 . З попередньої задачі маємо
. З попередньої задачі маємо 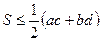 . Легко бачити, що виконується також нерівність
. Легко бачити, що виконується також нерівність 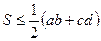 . Тоді
. Тоді
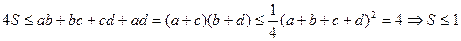 .
.
Цим самим фактично доведено, що з усіх опуклих чотирикутників із фіксованим периметром найбільшу площу має квадрат.
Задача 5.3.3. Довжини двох сторін трикутника 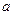 та
та 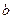 задовольняють умову
задовольняють умову  , а довжини відповідних їм висот дорівнюють
, а довжини відповідних їм висот дорівнюють 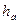 та
та 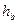 . Довести нерівність
. Довести нерівність 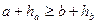 та встановити, коли досягається рівність.
та встановити, коли досягається рівність.
Доведення. Площа 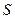 трикутника АВС дорівнює
трикутника АВС дорівнює 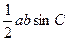 , звідки
, звідки 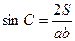 . Крім цього
. Крім цього  , звідки
, звідки 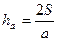 і
і 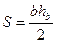 , звідки
, звідки 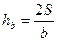 . Перетворимо нерівність, яку ми доводимо, наступним чином:
. Перетворимо нерівність, яку ми доводимо, наступним чином:
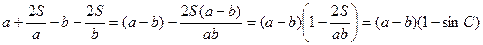 .
.
Очевидно, що, відповідно до умови задачі, одержаний вираз не може бути від’ємним. Легко бачити, що рівність досягається при 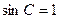 , тобто у випадку, коли трикутник прямокутний.
, тобто у випадку, коли трикутник прямокутний.