
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Застосування векторів
|
|
Інколи обґрунтування нерівності для відстаней зручно проводити, використовуючи вектори. При цьому може застосовуватися векторний аналог нерівності трикутника: 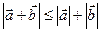 . У задачах, зв’язаних з центром ваги трикутника, використовується рівність
. У задачах, зв’язаних з центром ваги трикутника, використовується рівність 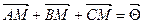 , де
, де 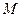 - точка перетину медіан,
- точка перетину медіан, 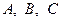 - вершини трикутника.
- вершини трикутника.
Задача 5.2.1. На площині задано два відрізки 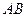 і
і 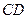 . Довести, що довжина відрізка, що сполучає їх середини, не більша за півсуму відрізків
. Довести, що довжина відрізка, що сполучає їх середини, не більша за півсуму відрізків 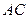 та
та 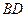 .
.
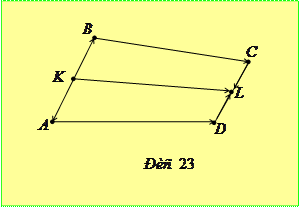 Доведення. Нехай точки
Доведення. Нехай точки 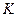 та
та 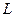 - середини відрізків
- середини відрізків  і
і 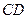 відповідно (рис. 23). Очевидно, що виконуються векторні рівності
відповідно (рис. 23). Очевидно, що виконуються векторні рівності 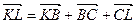 та
та 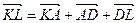 . Додаючи їх, отримуємо рівність
. Додаючи їх, отримуємо рівність 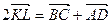 , з якої, переходячи до довжин векторів, дістаємо
, з якої, переходячи до довжин векторів, дістаємо 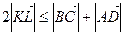 , що доводить висловлене в умові твердження. Знак рівності можливий при умові
, що доводить висловлене в умові твердження. Знак рівності можливий при умові 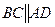 , тобто, коли заданий чотирикутник є трапецією або паралелограмом.
, тобто, коли заданий чотирикутник є трапецією або паралелограмом.
Задача 5.2.2. У чотирикутнику 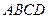 кут
кут 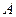 тупий,
тупий, 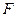 - середина сторони
- середина сторони  . Довести, що
. Довести, що 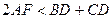 .
.
Доведення. Нехай точка 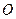 є серединою відрізка
є серединою відрізка 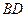 . Очевидно, що точка
. Очевидно, що точка 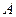 розташована всередині кола з діаметром
розташована всередині кола з діаметром 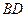 , тому
, тому 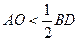 (
(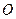 - центр кола). Оскільки
- центр кола). Оскільки 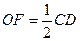 , як середня лінія трикутника
, як середня лінія трикутника 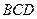 , то
, то 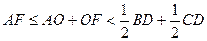 , що потрібно було довести.
, що потрібно було довести.
Задача 5.2.3. На площині задані два трикутники 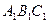 та
та 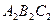 . Нехай
. Нехай 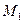 та
та 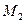 - точки перетину їхніх медіан. Довести, що
- точки перетину їхніх медіан. Довести, що 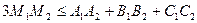 .
.
Доведення. Очевидно, що виконуються векторні рівності 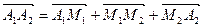 ,
,
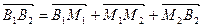 ,
,
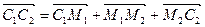 .
.
Додаючи їх, отримуємо  , звідки випливає нерівність, яку ми доводимо.
, звідки випливає нерівність, яку ми доводимо.
Задача 5.2.4. У піраміді  вершину
вершину 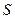 сполучили з точкою
сполучили з точкою 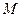 - центром ваги трикутника
- центром ваги трикутника  . Довести, що
. Довести, що 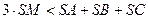 .
.
Доведення. Очевидно, що виконуються векторні рівності 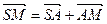 ,
, 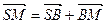 ,
, 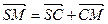 . Додаючи їх та враховуючи, що
. Додаючи їх та враховуючи, що 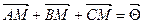 , отримуємо співвідношення
, отримуємо співвідношення 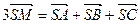 , з якого випливає задана нерівність. Знак рівності у ній неможливий, оскільки вектори
, з якого випливає задана нерівність. Знак рівності у ній неможливий, оскільки вектори 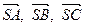 не колінеарні, тому
не колінеарні, тому  .
.