Геометричний спосіб доведення нерівностей між середніми квадратичним, арифметичним, геометричним та гармонічним

Задача 4.1.1. Довести нерівності між середнім квадратичним, арифметичним, геометричним та гармонічним у випадку двох чисел, тобто той факт, що для довільних виконуються співвідношення

.

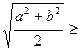
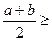
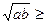
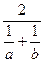Розв’язання. Наведемо один із можливих геометричних способів доведення.

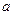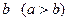Розглянемо трапецію з основами та . Позначимо через 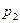середню лінію трапеції. Тоді 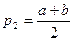буде середнім арифметичним чисел 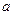та .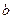

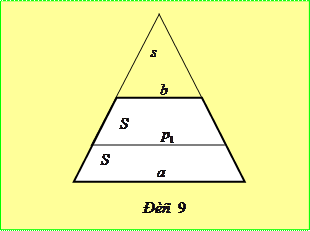
Відрізком 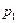, паралельним до основ трапеції, поділимо її на дві рівновеликі трапеції (рис. 9), площу кожної з яких позначимо через 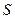. Продовжимо бічні сторони трапеції до перетину та позначимо площу трикутника, що утворився поза трапецією через 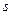. З подібності трьох трикутників, що утворилися, випливає пропорція 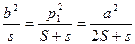. Звідси отримаємо рівність 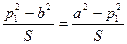або 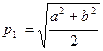. Таким чином, відрізок 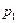є середнім квадратичним відрізків 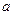та 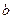. Середня лінія трапеції розташована вище від відрізка 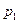, оскільки ділить трапецію на дві, з яких верхня має меншу площу, ніж нижня. Тому вона має меншу довжину, ніж відрізок 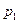. Цим самим показано, що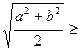 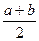, тобто, що середнє арифметичне не більше середнього квадратичного.

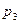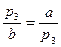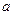Нехай відрізок паралельний до основ трапеції і ділить її на дві подібні трапеції. З подібності випливає пропорція , тобто є середнім геометричним чисел та .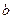

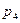Нехай відрізок паралельний до основ трапеції і проходить через точку перетину її діагоналей. З подібності трикутників легко встановити, що частини цього відрізка від точки перетину діагоналей трапеції до її бічних сторін рівні. Позначимо їх довжини через 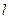, а частини довільної з діагоналей з кінцями у точці перетину діагоналей та у вершинах трапеції через 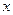та 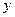(рис. 10).

З подібності трикутників отримуємо співвідношення 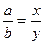та 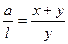, звідки 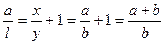. Тому 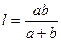і 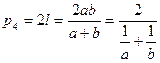, тобто 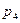є середнім гармонічним чисел 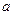та .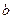

Тепер чисто геометрично легко показати, що відрізки задовольняють нерівності 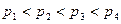, що завершує доведення алгебраїчних нерівностей.

Наведемо ще одне геометричне доведення нерівності Коші.

Задача 4.1.2. Довести, що 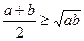, де .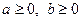

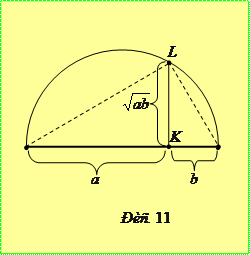Розв’язання. Нехай задані дрізки 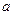та 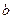. Побудуємо на відрізку 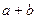, як на діаметрі, коло і у спільній для відрізків точці 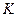проведемо перпендикуляр 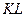до перетину з колом (рис. 11). З подібності прямокутних трикутників випливає, що 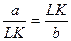, звідки 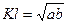. Очевидно, що цей відрізок не може перевищувати довжину радіуса кола, який дорівнює 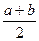. Тому .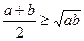