Область определения.

Областью определения называется множество, на котором задается функция.

Если задана функция, которая действует из одного множества в другое, то множество, из которого действует функция, называется областью определения.

Пусть задано отображение

f: X→ Y.

Множество X называется областью определения функции f и обозначается D(f).

Если функция задана параметрически, то

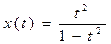
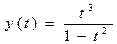
Найдем область определения для нашей кривой:

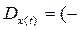
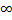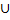; -1) 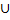(-1; 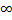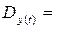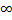1) (1; + )

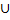(- ; -1) (-1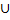; 1) (1; + )

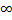Таким образом, 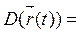(- 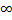; -1) (-1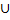; 1) (1; + ).

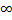" Концы": - 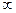, -1-0, -1+0, 1-0, 1+0, +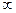

Область определения R, кроме t=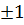

Получили, что кривая состоит из трёх ветвей

2.Симметрия относительно осей координат, начала координат и прямой y=x.

1) Симметрия относительно осей Ох и Oy.

Две точки А и А₁ называются симметричными друг другу относительно прямой m, если прямая m перпендикулярна отрезку АА₁ и проходит через его середину. Прямую m называют осью симметрии.

При сгибании плоскости чертежа по прямой m – оси симметрии симметричные фигуры совместятся.

Симметрия относительно оси Ox:

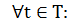x(t) = x(-t)

y(t) =- y(-t)

Если x(t) 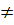x(-t) или y(t) 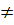-y(-t), то кривая не симметрична относительно оси Ox

Симметрия относительно оси Oy:

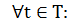x(t) = -x(-t)

y(t) =y(-t)

Если x(t) 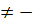x(-t) или y(t) 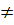y(-t), то кривая не симметрична относительно оси Oy.

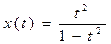
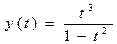
a) Относительно оси Ох. Достаточное условие симметрии:

x(-t)=x(t)

y(-t)=-y(t)

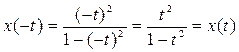
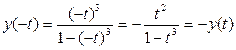
Следовательно, кривая симметрична относительно оси Ох.

b) Относительно оси Оу. Достаточное условие симметрии:

x(-t)=-x(t)

y(-t)=y(t)

т.е. х(t) не является нечетной.

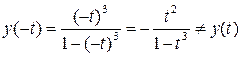, т.е. у(t) не является четной.

Таким образом, симметрия относительно Оy не установлена.

2) Симметрия относительно начала системы координат.

Достаточное условие симметрии:

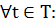x(t) = -x(-t)

y(t) = -y(-t)

Если x(t) 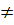-x(-t) или y(t) 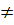-y(-t), то кривая не симметрична относительно начала системы координат.

По доказанному ранее уже известно, что x(t) является четной функцией, т.е.

x(-t)= x(t).

В связи с этим, симметрия относительно начала координат не установлена.

3) Симметрия относительно прямой у=х

Пусть М(х(t), y(t))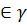

M´ симметрична М относительно прямой y=x

Тогда M (y(t), x(t))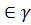

Это означает, что существует t₁: M (x(t₁), y(t₁))

t₁ – функция от t должна быть биекцией D на себя, тогда

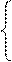x(t) = y(t₁)
y(t) = x(t₁)

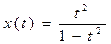
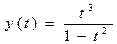
Чтобы определить симметрию относительно прямой y = x, нужно решить следующую систему:

→

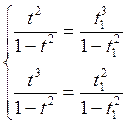
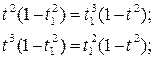
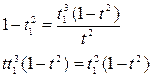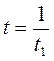
Если подставить в данную систему t = 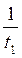, то система не имеет решение. Симметрия относительно прямой у=х не установлена.