
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Касательные, параллельные осям координат.
|
|
Пусть 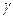 - гладкая кривая, заданная уравнением
- гладкая кривая, заданная уравнением 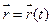 .
.
Зафиксируем точку 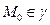 и рассмотрим произвольную прямую
и рассмотрим произвольную прямую  , проходящую через эту точку. Пусть
, проходящую через эту точку. Пусть 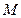 произвольная точка линии
произвольная точка линии 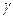 ,
,  – её расстояние до прямой
– её расстояние до прямой  .
.
Прямая  называется касательной к линии
называется касательной к линии 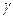 в точке
в точке 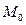 , если при стремлении
, если при стремлении 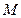 к
к 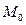 по линии
по линии 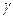 отношение
отношение 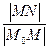 стремится нулю.
стремится нулю.
Имеет место
Т е о р е м а. Гладкая кривая имеет в каждой своей точке касательную, причем единственную.
При доказательстве этой теоремы расстояние 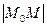 можно найти как длину вектора
можно найти как длину вектора 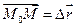 и использовать при этом формулу Тэйлора.
и использовать при этом формулу Тэйлора.
Расстояние  можно найти как высоту параллелограмма, построенного на векторе
можно найти как высоту параллелограмма, построенного на векторе 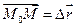 и направляющем орте
и направляющем орте 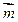 прямой
прямой  . Тоесть
. Тоесть 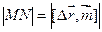 .
.
Тогда получим, что 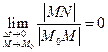 тогда и только тогда, когда
тогда и только тогда, когда 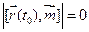 , то есть направляющий орт касательной
, то есть направляющий орт касательной 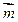 коллинеарен вектору
коллинеарен вектору  . Таким образом, направляющим вектором касательной к гладкой кривой в точке
. Таким образом, направляющим вектором касательной к гладкой кривой в точке 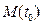 является вектор
является вектор  .
.
а) горизонтальные:
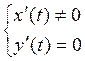
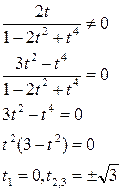
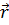 (0)=(0; 0)
(0)=(0; 0)
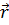 (
(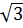 ) =(
) =(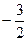 ;
; 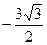 )
)
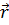 (
(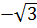 )=(
)=(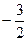 ;
; 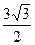 )
)
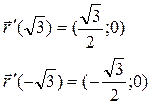
В этих точках горизонтальные касательные касаются графика функции 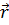 (t).
(t).
б) вертикальные
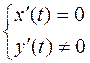
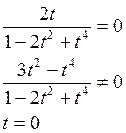
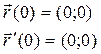
В этих точках вертикальные касательные касаются графика функции 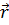 (t).
(t).