
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретические сведения. Для двух игроков А и В задана платежная матрица
|
|
Для двух игроков А и В задана платежная матрица
| Стратегии игрока B | ||||||
| B1 | B2 | B3 | B4 | B5 | ||
| Стратегии игрока A | A1 | -2 | -1 | |||
| A2 | -1 | -2 | ||||
| A3 | -1 | |||||
| A4 | -1 | |||||
| A5 | -1 | -1 | -1 |
Игрок А использует логику, которая гарантирует ему максимальный выигрыш вне зависимости от поведения игрока В.
Определяются минимальные элементы каждой строки, что соответствует минимальным выигрышам игрока А при каждой стратегии и среди них, находится максимальное число, равное -1.
Таким образом, свой выбор, игрок А остановит на стратегии A3, которая обеспечит ему выигрыш -1, т.е. потерю не более 1 ден.ед.
Значение равное -1, называется нижней ценой игры.
| Стратегии игрока B | Минимальный элемент в строке | ||||||
| B1 | B2 | B3 | B4 | B5 | |||
| Стратегии игрока A | A1 | -2 | -1 | -2 | |||
| A2 | -1 | -2 | -2 | ||||
| A3 | -1 | -1 | |||||
| A4 | -1 | -1 | |||||
| A5 | -1 | -1 | -1 | -1 |
Игрок В использует логику, которая гарантирует ему минимальный проигрыш вне зависимости от поведения игрока А.
Определяются максимальные элементы каждого столбца, что соответствует максимальным проигрышам игрока В при каждой стратегии и среди них, находится минимальное число, равное 1.
Свой выбор, игрок В остановит на стратегии В3, которая обеспечит ему проигрыш 1, т.е. потерю не более 1 ден.ед.
Значение равное 1, называется верхней ценой игры.
| Стратегии игрока B | Минимальный элемент в строке | ||||||
| B1 | B2 | B3 | B4 | B5 | |||
| Стратегии игрока A | A1 | -2 | -1 | -2 | |||
| A2 | -1 | -2 | -2 | ||||
| A3 | -1 | -1 | |||||
| A4 | -1 | -1 | |||||
| A5 | -1 | -1 | -1 | -1 | |||
| Максимальный элемент в столбце |
Если верхняя цена игры равна нижней цене игры (седловая точка), то было бы найдено решение, которое устраивает обоих игроков, исходя из их логики. В рассматриваемом примере, если игроки пользуются только чистыми стратегиями, оптимальное решение не найдено. Но, всегда есть решение в смешанных стратегиях.
Смешанной стратегией игрока А называется применение чистых стратегий A1, A2, A3, A4, A5 c вероятностями p1, p2, p3, p4, p5.
Смешанную стратегию первого игрока обозначают как вектор
P = (p1, p2, p3, p4, p5),
где p1 + p2 + p3 + p4 + p5 = 1; p1, p2, p3, p4, p5 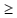 0.
0.
Смешанной стратегией игрока B называется применение чистых стратегий B1, B2, B3, B4, B5 c вероятностями q1, q2, q3, q4, q5.
Смешанную стратегию второго игрока обозначают как вектор
Q = (q1, q2, q3, q4, q5),
где q1 + q2 + q3 + q4 + q5 = 1 и q1, q2, q3, q4, q5 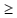 0
0
Оптимальное решение игры (или просто - решение игры) - это пара оптимальных смешанных стратегий
P* (p*1, p*2, p*3, p*4, p*5) и Q* (q*1, q*2, q*3, q*4, q*5),
Таким образом, если один из игроков придерживается своей оптимальной стратегии, то другому невыгодно отступать от своей стратегии.
Выигрыш игрока А равный проигрышу игрока В, соответствующий оптимальному решению, называется ценой игры v.
Цена игры больше либо равна нижней цены игры и меньше или равна верхней цены игры, т.е. -1 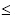 v
v 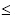 1.
1.
Исходную платежную матрицу можно уменьшить, если исключить из нее стратегии, которыми заведомо не выгодно пользоваться игрокам.
| Стратегии игрока B | ||||||
| B1 | B2 | B3 | B4 | B5 | ||
| Стратегии игрока A | A1 | -2 | -1 | |||
| A2 | -1 | -2 | ||||
| A3 | -1 | |||||
| A4 | -1 | |||||
| A5 | -1 | -1 | -1 |
1. Стратегия A4 является доминирующей над стратегией A1, т.к. каждый элемент строки 4 больше или равен соответствующего элемента строки.
Игроку А заведомо не выгодно пользоваться стратегией A1. Удаляем стратегию A1 из рассмотрения.
| Стратегии игрока B | ||||||
| B1 | B2 | B3 | B4 | B5 | ||
| Стратегии игрока A | A2 | -1 | -2 | |||
| A3 | -1 | |||||
| A4 | -1 | |||||
| A5 | -1 | -1 | -1 |
2. Стратегия A3 является доминирующей над стратегией A5, поэтому удаляем стратегию A5 из рассмотрения.
| Стратегии игрока B | ||||||
| B1 | B2 | B3 | B4 | B5 | ||
| Стратегии игрока A | A2 | -1 | -2 | |||
| A3 | -1 | |||||
| A4 | -1 |
3. Стратегия B4 является доминирующей над стратегией B5. Удаляется стратегия B5 из рассмотрения.
| Стратегии игрока B | ||||
| B1 | B3 | B4 | ||
| Стратегии игрока A | A2 | -1 | -2 | |
| A3 | -1 | |||
| A4 | -1 |
4. Игроку А заведомо не выгодно пользоваться стратегией A2. Удаляется стратегия A2 из рассмотрения.
| Стратегии игрока B | ||||
| B1 | B3 | B4 | ||
| Стратегии игрока A | A3 | -1 | ||
| A4 | -1 |
После преобразований платежной матрицы, оптимальное решение будем искать в виде:
P* = (0, 0, p*3, p*4, 0),
Q* = (q*1, 0, q*3, q*4, 0).
В задаче, значение цены игры определяется неравенством -1 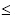 v
v 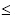 1. В дальнейшем, потребуется, чтобы цена игры была положительной, для этого воспользуемся следующей теоремой.
1. В дальнейшем, потребуется, чтобы цена игры была положительной, для этого воспользуемся следующей теоремой.
Если к каждому элементу платежной матрицы прибавить положительное число, то цена игры увеличится на это число, при этом оптимальное решение игры не изменится. Если все элементы матрицы больше или равны нулю, то и цена игры будет положительной.
Таким образом, необходимо ко всем элементам матрицы прибавить число, равное по модулю наименьшему элементу матрицы.
Прибавим 1 к каждому элементу матрицы. Тогда, цена исходной игры v = v1 -1, где v1 - цена игры новой матрицы.
| Стратегии игрока B | ||||
| B1 | B3 | B4 | ||
| Стратегии игрока A | A3 | |||
| A4 |
Если P* = (0, 0, p*3, p*4, 0) и Q* = (q*1, 0, q*3, q*4, 0) являются оптимальным решением, то должны выполняться две следующие системы неравенств:
8 p*3 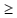 v1
v1
2 p*3 + p*4 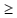 v1
v1
4 p*4 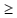 v1
v1
и
8 q*1 + 2 q*3 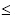 v1
v1
q*3 + 4 q*4 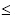 v1
v1
Рассмотрим первую систему.
Разделим все члены системы на цену игры v1. Знаки в неравенствах системы не изменятся, так как цена игры положительная.
Введем новые обозначения:
y1 = p*3 / v1, y2 = p*4 / v1
Рассмотрим сумму:
y1 + y2 = p*3 / v1 + p*4 / v1 = 1/v1 * (p*3 + p*4) = 1/v1,
где (p*3 + p*4)=1 (сумма вероятностей используемых стратегий равна единице).
Игрок A старается увеличить свой выигрыш, т.е. цену игры v1, поэтому выражение 1/v1 будет стремиться к минимуму. Таким образом, из первой системы будет получена задача линейного программирования.
Требуется найти минимум линейной функции
F = y1 + y2
при следующей системе ограничений:
8 y1 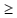 1
1
2 y1 + y2 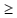 1
1
4 y2 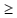 1
1
Рассмотрим вторую систему.
Разделим все члены системы на цену игры v1. Знаки в неравенствах системы не изменятся, так как цена игры положительная.
Введем новые обозначения:
x1 = q*1 / v1, x2 = q*3 / v1, x3 = q*4 / v1
Рассмотрим сумму:
x1 + x2 + x3 = q*1 / v1 + q*3 / v1 + q*4 / v1 = 1/v1 * (q*1 + q*3 + q*4) = 1/v1
Игрок B старается уменьшить свой проигрыш, т.е. цену игры v1, поэтому выражение 1/v1 будет стремиться к максимуму. Таким образом, из первой системы будет получена задача линейного программирования.
Требуется найти максимум линейной функции
L = x1 + x2 + x3
при следующей системе ограничений:
8 x1 + 2 x2 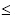 1
1
x2 + 4 x3 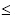 1
1
Полученные задачи являются парой симметричных взаимно двойственных задач.
Если решить одну из этих задач, то автоматически будет получено решение второй.
Для решения воспользуемся симплекс-методом, реализованного в виде надстройки Excel Поиск решений (лабораторная работа 3).
В книге Поиск решений на странице Таблица с формулами последовательно внести данные первой и второй систем и найти решение. Предварительно изменить формат ячеек для переменных и целевой функции на числовой с двумя знаками после запятой.
Решение для первой задачи
y1 = 0, 38; y2 = 0, 25; F = 0, 63.
Решение для второй задачи
х1 = 0; х2 = 0, 5; х3 = 0, 13; L = 0, 63.
Максимальное значение функции прямой задачи равно минимальному значению функции двойственной задачи.
Найдем цену игры v1.
v1 = 1 / F = 1 / L = 1/0, 63 = 1, 6
Так как к каждому элементу матрицы мы прибавили 1, следовательно, цена исходной игры равна:
v = v1 - 1 = 1, 6 - 1 = 0, 6.
Теперь можно найти оптимальное решение игры.
Вероятности стратегий игрока А.
p*1 = 0;
p*2 = 0;
p*3 = y1 * v1 = 0, 38 * 1, 6 = 0, 6;
p*4 = y2 * v1 = 0, 25 * 1, 6 = 0, 4;
p*5 = 0;
P* = (0; 0; 0, 6; 0, 4; 0);
Цена игры v = 0, 6.
Вероятности стратегий игрока В.
q*1 = x1 * v1 = 0 * 1, 6 = 0;
q*2 = 0;
q*3 = x2 * v1 = 0, 5 * 1, 6 = 0, 8;
q*4 = x3 * v1 = 0, 13 * 1, 6 = 0, 2;
q*5 = 0.
Q* = (0; 0; 0, 8; 0, 2; 0)
Цена игры v = 0, 6.
Анализ результата решения задачи.
Выигрыш игрока А составит 3/5 денежных единиц, а проигрыш игрока В составит ту же сумму (игра с нулевой суммой).
Игрок А использует свои стратегии следующим образом:
- A1 на 0 %
- A2 на 0 %
- A3 на 60 %
- A4 на 40 %
- A5 на 0 %
Игрок B использует свои стратегии следующим образом:
- B1 на 0 %
- B2 на 0 %
- B3 на 80 %
- B4 на 20 %
- B5 на 0 %