
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
По результатам расчетов будем формировать таблицу 1 (последовательно заносим результаты, полученные по различным критериям).
|
|
| Байеса | Лапласа | Вальда | Гурвица | Ходжа-Лемана | |
| А1 | -3 | -0, 6 | |||
| А2 | 3, 5 | 2, 7 | -1 | 2, 6 | 1, 7 |
| А3 | 4, 2 | -7 | -0, 28 | ||
| Принимаемое решение | А3 | А2 | А2 | А3 | А2 |
Критерий Байеса (максимального математического ожидания)
Расчет осуществляется по формуле:
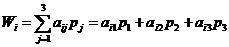 ;
;
W1 = 2∙ 0, 2 + (-3) ∙ 0, 5 + 7∙ 0, 3 = 0, 4 – 1, 5 + 2, 1 = 1
W2 = -1∙ 0, 2 + 5 ∙ 0, 5 + 4∙ 0, 3 = -0, 2 + 2, 5 + 1, 2 = 3, 5
W3 = -7∙ 0, 2 + 13 ∙ 0, 5 + (-3)∙ 0, 3 = -1, 2 + 6, 5 - 0, 9 = 4, 2
Находим максимальное значение из полученных значений математического ожидания W = max{1; 3.5; 4.2} = 4.2.
Таким образом, оптимальной по данному критерию является стратегия А3 – продавать в весенние месяцы.
Критерий Лапласа (недостаточного основания)
Находим среднее значение элементов каждой строки:
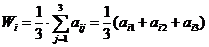 .
.
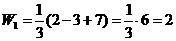
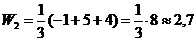
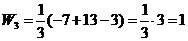 .
.
Определяется максимальное значение W = max{2; 2.7; 1} = 2.7.
Оптимальной по данному критерию является стратегия А2 – продавать в зимние месяцы.
Критерий Вальда (максиминный)