
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приклад 1. Перевірка наявності тенденції.
|
|
Дослідити часовий ряд на наявність тренду (тенденції). Умовні дані про витрати на впровадження інновацій в попередньому періоді, тис грн. (Y).
Вхідні дані та обчислення оформимо у таблиці (табл. 4.1).
Обчислення:
Крок 1. Вхідний часовий ряд у1 , у2, у3, …, ул розбиваємо на дві приблизно рівні частини обсягом п1 ≈ п2: п1 = 13, п2 = 12,
(п1 + п2 = п).
Крок 2. Для кожної з частин обчислюють середні значення та дисперсії:

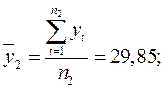
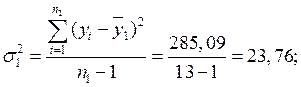
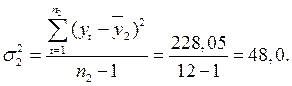
Таблиця 4.1
| t (рік) | Витрати на впровадження інновацій в попередньому періоді, тис грн. | ||
| x | y | yt–yсереднє | |
| 3, 52 | -9, 52 | ||
| 9, 7 | -3, 34 | ||
| 8, 9 | -4, 14 | ||
| 9, 8 | -3, 24 | ||
| 10, 1 | -2, 94 | ||
| 13, 9 | 0, 86 | ||
| 19, 9 | 6, 86 | ||
| 14, 3 | 1, 26 | ||
| 11, 5 | -1, 54 | ||
| 19, 5 | 6, 46 | ||
| 14, 2 | 1, 16 | ||
| 0, 96 | |||
| 20, 2 | 7, 16 | 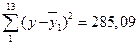
| |
| 22, 7 | -7, 15 | ||
| 28, 2 | -1, 65 | ||
| 25, 2 | -4, 65 | ||
| -4, 85 | |||
| 24, 3 | -5, 55 | ||
| 21, 5 | -8, 35 | ||
| 27, 1 | -2, 75 | ||
| 36, 3 | 6, 45 | ||
| 34, 1 | 4, 25 | ||
| 34, 1 | 4, 25 | ||
| 35, 2 | 5, 35 | ||
| 44, 5 | 14, 65 | 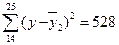
| |
| Разом | 527, 72 |
Крок 3. Висуваємо основну гіпотезу про рівність середніх значень:
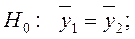
проти альтернативної 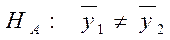
Нульову гіпотезу відхиляємо: 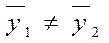 .
.
Та допоміжну гіпотезу про рівність дисперсій
проти альтернативної 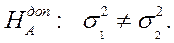
Допоміжну нульову гіпотезу про рівність дисперсій відхиляємо: 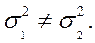
Крок 4. Перевіряємо допоміжну гіпотезу за допомогою F-критерію Фішера. Для цього порівняємо розрахункове (експериментальне) значення критерію з табличним (критичним) значенням розподілу Фішера: 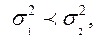 тому
тому 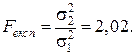
Fтабл = F(а, k1, k2) = 2, 82,
при a=0, 05 – заданий рівень значущості,
k1= п1 –1=13–1=12,
k2= п2 –1=12–1=11.
За критерієм Фішера Fексп < Fтабл.
Переходимо до наступного пункту.
Крок 5. Основну гіпотезу про відсутність тренда перевіряють за допомогою t-критерію Стьюдента. Обчислимо вибіркову статистику – розрахункове значення критерію Стьюдента за формулою
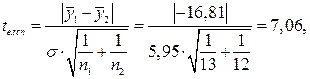
де s – середньоквадратичне відхилення різниці середніх.
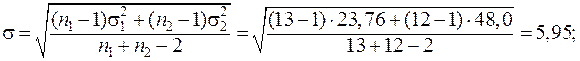
tтабл = 2, 069,
де tтабл =t(а, (п– 2)).
Розрахункове значення tексп > tтабл. Основна гіпотеза Н0відхиляється. Отже, ряд має тренд.
Висновок. Нульова гіпотеза (H0) відхиляється, ряд має тенденцію до змінювання (тренд є).