
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Перевірка значимості коефіцієнта детермінації, коефіцієнта кореляції та оцінок параметрів моделі множинної регресії.
|
|
Перевірка значимості коефіцієнта детермінації
Висувається нульова гіпотеза H0: R2=0,
або H0: b1 = b2 =... = bn = 0.
Альтернативна до неї є НА: (bj ≠ 0)
За отриманими в моделі значеннями коефіцієнта детермінації R2обчислюємо експериментальне значення F-статистики:
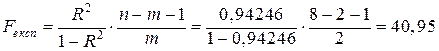
Визначимо табличне значення F-критерію Фішера:
| Fтабл = | 3, 9715 | ||
| =FРАСПОБР(0, 05; 5; 7) | |||
Порівняємо з табличним значенням розподілу Фішера при ступенях вільності f1 = n–m–1, f2 = n–1 та рівні значущості a= 0, 05:
Fексп > Fтабл
Нульова гіпотеза відхиляється.
Відхилення нуль-гіпотези свідчить про значимість коефіцієнта детермінації.
Перевірка значимості коефіцієнта кореляції
Коефіцієнт кореляції, як вибіркова характеристика, перевіряється на значущість за допомогою t-критерію Ст’юдента при k=n–m1 ступенях вільності тарівні значимості a=0, 05.

| tтабл = | 2, 57058 | ||
| =СТЬЮДРАСПОБР(0, 05; 5) | |||
Величина експериментального значення t-статистики перевищує табличне:
|tексп| > tтабл
9, 049 > 2, 57058
Тобто можна зробити висновок, що коефіцієнт кореляції достовірний (значущий), а зв'язок між залежною змінною та всіма незалежними факторами суттєвий.
Перевірка значимості оцінок параметрів моделі
множинної регресії
Для оцінки значимості кожного параметра моделі перевіряємо їх за допомогою t-критерію Ст’юдента:
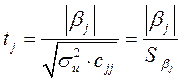
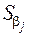 де сjj – діагональний елемент матриці (Х' Х)-1;
де сjj – діагональний елемент матриці (Х' Х)-1;
– стандартна похибка оцінки параметра моделі.
Статистичну значущість кожного параметра моделі можна перевірити за допомогою t-критерію. При цьому нульова гіпотеза має вигляд:
Н0 : bj = 0,
альтернативна
НА : bj ≠ 0.
Будемо наслідувати відповідний алгоритм. Задамо рівень значущості a=0, 05, визначимо табличне значення t-критерію Ст’юдента (tтабл =2, 5058) і розрахуємо значення t-критерію для кожного параметра.
| Перевірка гіпотези Н0: b0 =0 | |
| tспос = | 9, 4678 |
| Перевірка гіпотези Н0: b1 =0 | |
| tспос = | 4, 1439 |
| Перевірка гіпотези Н0: b2 =0 | |
| tспос = | 2, 4435 |
| Якщо | tспос | < tтабл , то приймаємо гіпотезу Н0. |
| Якщо | tспос | > tтабл , то відхиляємо гіпотезу Н0. |
Перевіряємо виконання нерівності | tспос | > tтабл робимо висновки про стійкість впливу відповідного параметру на залежну змінну Y:
| для b0: |9, 4678| > 2, 57058 → Н0 (b0=0) відхиляємо; змінна X0 (вільний член) є значущою; |
| для b1: |4, 1439| > 2, 57058 → Н0 (b1=0) відхиляємо; змінна Х1 (вартість основних засобів) є значущою; |
| для b2: |2, 4435| < 2, 57058 → Н0, (β 2=0) приймаємо; змінна Х2, (чисельність працюючих) є незначущою. |
Знайдемо інтервали надійності для кожного окремого параметра за формулою:

| = 23, 89 – 2, 57 * 2, 523 < b0 < 23, 89 + 2, 57 * 2, 523 |
| = 0, 97 – 2, 57 * 0, 235 < b1 < 0, 97 + 2, 57 * 0, 235 |
| = 0, 38 – 2, 57 * 0, 155 < b2 < 0, 38 + 2, 57 * 0, 155 |
P (17, 4 < b0 < 30, 37) = 0, 95
P (0, 37 < b1 < 1, 579) = 0, 95
P (–0, 02 < b2 < 0, 779) = 0, 95
3. Обчислимо прогнозні значення Yпр:
У рівняння Yрозр = 23, 89 +0, 97X1 +0, 38X2 підставимо прогнозні значення фактору Хпр = (1, 15, 35), що лежить за межами базового періоду (точковий прогноз):
Yпр = 23, 89 + 0, 97 × 15 + 0, 38 × 35 = 51, 79
Тоді M(Yпр) можна розглядати як оцінку прогнозного значення математичного сподівання та індивідуального значення обсягу виробленої продукції при відомих параметрах вартості основних засобів (Х1) та чисельності працюючих (Х2).
Визначимо дисперсію прогнозу  з урахуванням матриці похибок, яка для прикладу має вигляд:
з урахуванням матриці похибок, яка для прикладу має вигляд:
| (Х' × Х)–1 = | 3, 78969 | 0, 12007 | –0, 20478 |
| 0, 12007 | 0, 03291 | –0, 01593 | |
| –0, 20478 | –0, 01593 | 0, 01438 |
Елементи дисперсійно-ковартційної матриці, які розраховуються за формулами і мають значення:
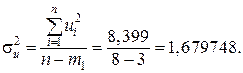
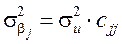
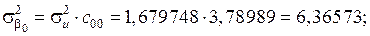

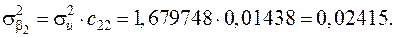

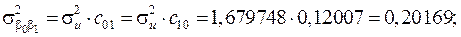
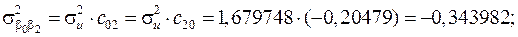
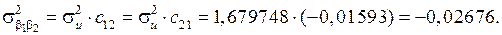
| 6, 36573 | 0, 20169 | –0, 343982 | |
| var (В) = | 0, 20169 | 0, 05529 | –0, 02676 |
| –0, 343982 | –0, 02676 | 0, 02415 |
| Хпр = | |
| Х'пр = |
| Х'пр * var (В) = | –2, 6483 | 0, 0944 | 0, 0999 |
Знайдемо дисперсію прогнозу:
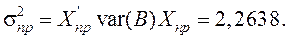
Середньоквадратична похибка прогнозу математичного сподівання M(Y np):
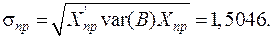
Довірчий інтервал для математичного сподівання M(Y np) прогнозного значення розрахуємо за формулою:

де t – табличне значення t-критерію Ст’юдента з ступенем вільності k=n–m1 тарівнем значимості a=0, 05.
51, 79 – 2, 57058 × 1, 5046 ≤ M(Yпр) ≤ 51, 79 + 2, 57058 × 1, 5046
| 47, 9264 | ≤ M(Yпр) ≤ | 55, 6617 |
Знайдемо межі інтервального прогнозу індивідуального значення Yпр:
Для цього обчислимо дисперсію та стандартну похибку прогнозу індивідуального значення Yпр:
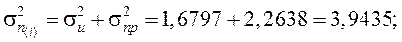
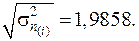
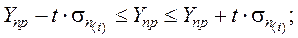
51, 79 – 2, 57058 × 1, 9858 ≤ Yпр ≤ 51, 79 + 2, 57058 × 1, 9858
| 46, 6893 | ≤ Yпр ≤ | 56, 8988 |
4. Графічне зображення моделі ґрунтується на побудові ліній регресії, в прямокутних координатах Y – x1 та Y – x2 (рис. 6.1).
При цьому масштаб треба обрати таким, щоб мінімальні та максимальні значення x1 та x2 співпадали між собою.
Лінія регресії Y= f (X1) при X2=const відображає вплив першого фактора х1 на продуктивність праці при постійному значенні другого х2 (середнє значення х2).
Лінія регресії Y= f (X2) при X1=const відображає вплив другого фактора х2 на продуктивність праці при постійному значенні х1 (середнє значення х1).
| X1 | X2 | Y=f(X1) при X2=const | Y=f(X2) при X1=const | Середні значення | ||
| min | 4, 20 | 13, 00 | 30, 64 | 35, 64 | X1 | X2 |
| max | 14, 20 | 28, 00 | 40, 38 | 41, 34 | 7, 00 |
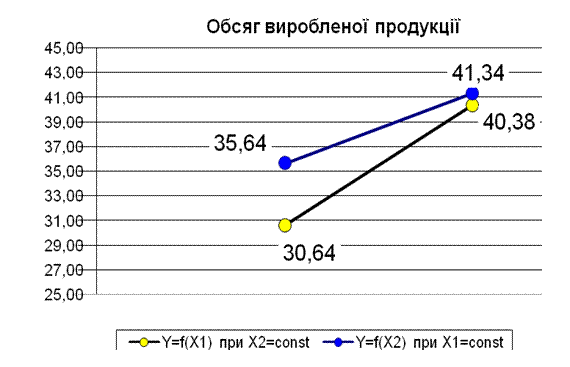
Рис. 6.1. Графічне зображення моделі