
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейная парная регрессия.
|
|
Наиболее простой с точки зрения понимания, интерпретации и техники расчетов является линейная форма регрессии.
Уравнение линейной парной регрессии 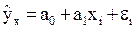 , где
, где
a0, a1– параметры модели, ε i – случайная величина (величина остатка).
Параметры модели и их содержание:
Ø a0 – свободный коэффициент (член) регрессионного уравнения. Не имеет экономическою смысла и показывает значение результативного признака y, если факторный признак x =0.
Ø a1 - коэффициент регрессии показывает, на какую величину в среднем изменится результативный признак y, если переменную х увеличить на единицу измерения. Знак при коэффициенте регрессии показывает направление связи: при a1 > 0 – связь прямая; при a1 < 0 - связь обратная.
Ø ε i- независимая, нормально распределенная случайная величина. Отражает тот факт, что изменение y будет неточно описываться изменением x, так как присутствуют другие факторы, не учтенные в данной модели.
Оценка параметров модели а0 и а, осуществляется методом наименьших квадратов.
Система нормальных уравнений для нахождения параметра линейной парной регрессии методом наименьших квадратов

Формулы для определения значения параметров a0 и a1

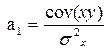 , где
, где
 – ковариация признаков
– ковариация признаков 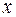 и
и  ,
,
Ковариацияпризнаков характеризует сопряженность вариации двух признаков и представляет собой статистическую меру взаимодействия двух случайных переменных.
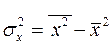 – дисперсия признака
– дисперсия признака 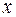 ,
,
Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности.
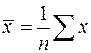 ,
, 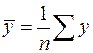 ,
,  ,
, 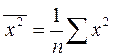 .
.
Уравнение регрессии дополняется показателем тесноты связи между признаками - линейным коэффициентом корреляции 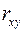 , который рассчитывают по формуле:
, который рассчитывают по формуле:
 или
или  .
.
Коэффициент корреляции принимает значение от -1 до +1. Положительное значение коэффициента свидетельствует о наличии прямой связи, отрицательное значение — обратной. Если rух = ±1, корреляционная связь представляется линейной функциональной зависимостью. При rух = 0 линейная корреляционная связь отсутствует.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 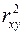 , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака
, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака  , объясняемую регрессией, в общей дисперсии результативного признака:
, объясняемую регрессией, в общей дисперсии результативного признака:
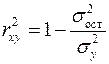 ,
,
где

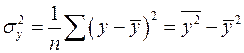 .
.
Соответственно величина 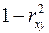 характеризует долю дисперсии
характеризует долю дисперсии  , вызванную влиянием остальных, неучтенных в модели, факторов.
, вызванную влиянием остальных, неучтенных в модели, факторов.
Оценка значимости уравнения регрессии в целом производится на основе 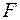 - критерия Фишера
- критерия Фишера
В случае парной линейной регрессии значимость модели регрессии определяется по следующей формуле: 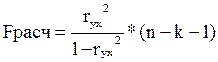 .
.
Если при заданном уровне значимости расчетное значение F -критерия с γ 1=k, γ 2=(п – k – 1) степенями свободы больше табличного, то модель считается значимой, гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.
Для оценки статистической значимости коэффициентов регрессии и корреляции производят расчет 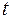 -критерий Стьюдента и доверительные интервалы каждого из показателей.
-критерий Стьюдента и доверительные интервалы каждого из показателей.
Порядок расчетов:
1. Расчет случайных ошибок параметров линейной регрессии и коэффициента корреляции

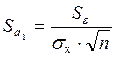
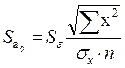

2. Расчет фактических значений t-статистик
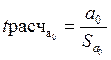
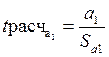
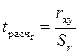
Расчетные значения t-критерия сравнивают с табличным значением критерия t α γ ,.которое определяется при (n — k — 1) степенях свободы и соответствующем уровне значимости α. Если расчетное значение t -критерия превосходит его табличное значение t α γ , то параметр признается значимым.
В качестве меры точности модели применяют точностные характеристики: Для определения меры точности модели рассчитывают:
Ø максимальная ошибка - соответствует отклонению расчетному отклонению расчетных значений от фактических
Ø средняя абсолютная ошибка – ошибка показывает, насколько в среднем отклоняются фактические значения от модели
Ø дисперсия ряда остатков (остаточная дисперсия)
Ø средняя квадратическая ошибка. Представляет собой корень квадратный из дисперсии, чем меньше значение ошибки, тем точнее модель
Ø средняя относительная ошибка аппроксимации.
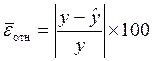
Средняя ошибка аппроксимации не должна превышать 8–10%.
Если модель регрессии признана адекватной, а параметры модели значимы, то переходят к построению прогноза.
Прогнозируемое значение переменной у получается при подстановке в уравнение регрессии ожидаемой величины независимой переменной х прогн.

Данный прогноз называется точечным. Вероятность реализации точечного прогноза практически равна нулю, поэтому рассчитывается доверительный интервал прогноза с большой надежностью.
Доверительные интервалы прогноза зависят от стандартной ошибки, удаления х прогн от своего среднего значения  , количества наблюдений n и уровня значимости прогноза α. Доверительные интервалы прогноза рассчитывают по формуле:
, количества наблюдений n и уровня значимости прогноза α. Доверительные интервалы прогноза рассчитывают по формуле:
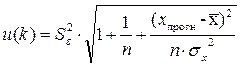 где
где
t табл – определяется по таблице распределения Стьюдента для уровня значимости α и числа степеней свободы γ =n-k-1.
Пример13.
По данным проведенного опроса восьми групп семей известны данные связи расходов населения на продукты питания с уровнем доходов семьи
Расходы на продукты питания,  , тыс. руб. , тыс. руб.
| 0, 9 | 1, 2 | 1, 8 | 2, 2 | 2, 6 | 2, 9 | 3, 3 | 3, 8 |
Доходы семьи, 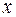 , тыс. руб. , тыс. руб.
| 1, 2 | 3, 1 | 5, 3 | 7, 4 | 9, 6 | 11, 8 | 14, 5 | 18, 7 |
Решение:
Предположим, что связь между доходами семьи и расходами на продукты питания линейная. Для подтверждения нашего предположения построим поле корреляции.
Для удобства дальнейших вычислений составим таблицу 37.
Рассчитаем параметры линейного уравнения парной регрессии 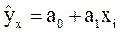 .
.


Уравнение регрессии:
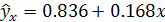
Т.е. с увеличением дохода семьи на 1000 руб. расходы на питание увеличиваются на 168 руб.
Расчет линейного коэффициента корреляции 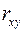 :
:

Близость коэффициента корреляции к 1 указывает на тесную линейную связь между признаками.

| 
| 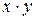
| 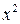
| 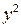
| 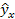
| 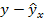
| 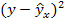
| 
| |
| 1, 2 | 0, 9 | 1, 08 | 1, 44 | 0, 81 | 1, 038 | –0, 138 | 0, 0190 | 15, 33 | |
| 3, 1 | 1, 2 | 3, 72 | 9, 61 | 1, 44 | 1, 357 | –0, 157 | 0, 0246 | 13, 08 | |
| 5, 3 | 1, 8 | 9, 54 | 28, 09 | 3, 24 | 1, 726 | 0, 074 | 0, 0055 | 4, 11 | |
| 7, 4 | 2, 2 | 16, 28 | 54, 76 | 4, 84 | 2, 079 | 0, 121 | 0, 0146 | 5, 50 | |
| 9, 6 | 2, 6 | 24, 96 | 92, 16 | 6, 76 | 2, 449 | 0, 151 | 0, 0228 | 5, 81 | |
| 11, 8 | 2, 9 | 34, 22 | 139, 24 | 8, 41 | 2, 818 | 0, 082 | 0, 0067 | 2, 83 | |
| 14, 5 | 3, 3 | 47, 85 | 210, 25 | 10, 89 | 3, 272 | 0, 028 | 0, 0008 | 0, 85 | |
| 18, 7 | 3, 8 | 71, 06 | 349, 69 | 14, 44 | 3, 978 | –0, 178 | 0, 0317 | 4, 68 | |
| Итого | 71, 6 | 18, 7 | 208, 71 | 885, 24 | 50, 83 | 18, 717 | –0, 017 | 0, 1257 | 52, 19 |
| Ср. Знач. | 8, 95 | 2, 34 | 26, 09 | 110, 66 | 6, 35 | 2, 34 | – | 0, 0157 | 6, 52 |

| 5, 53 | 0, 935 | – | – | – | – | – | – | – |

| 30, 56 | 0, 874 | – | – | – | – | – | – | – |
Расчет коэффициента детерминации 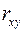 :
:
Коэффициент детерминации 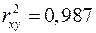 показывает, что уравнением регрессии объясняется 98, 7% дисперсии результативного признака, а на долю прочих факторов приходится лишь 1, 3%.
показывает, что уравнением регрессии объясняется 98, 7% дисперсии результативного признака, а на долю прочих факторов приходится лишь 1, 3%.
Оценим качество уравнения регрессии в целом с помощью 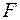 -критерия Фишера. Произведем расчет фактического значения
-критерия Фишера. Произведем расчет фактического значения 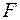 -критерия:
-критерия:
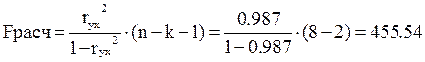
Табличное значение ( ,
, 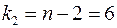 ,
, 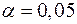 ):
): 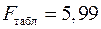 . Т. к.
. Т. к.  , то признается статистическая значимость уравнения в целом.
, то признается статистическая значимость уравнения в целом.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитаем 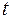 -критерий Стьюдента и доверительные интервалы каждого из показателей. Рассчитаем случайные ошибки параметров линейной регрессии и коэффициента корреляции
-критерий Стьюдента и доверительные интервалы каждого из показателей. Рассчитаем случайные ошибки параметров линейной регрессии и коэффициента корреляции
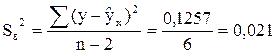

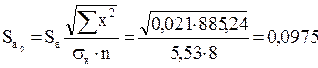

Фактические значения 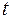 -статистик:
-статистик:



Табличное значение 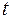 -критерия Стьюдента при
-критерия Стьюдента при 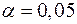 и числе степеней свободы
и числе степеней свободы  есть
есть  . Так как
. Так как  , то признаем статистическую значимость параметров регрессии и показателя тесноты связи.
, то признаем статистическую значимость параметров регрессии и показателя тесноты связи.
Рассчитываем среднюю ошибку аппроксимации:  , вычисления заносим в таблицу ст.10
, вычисления заносим в таблицу ст.10
 говорит о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе модели к исходным данным.
говорит о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе модели к исходным данным.
Рассчитываем прогнозное значение результативного фактора 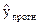 при значении признака-фактора, составляющем 110% от среднего уровня
при значении признака-фактора, составляющем 110% от среднего уровня
 , т.е. найдем расходы на питание, если доходы семьи составят 9, 85 тыс. руб.
, т.е. найдем расходы на питание, если доходы семьи составят 9, 85 тыс. руб.

Значит, если доходы семьи составят 9, 845 тыс. руб., то расходы на питание будут 2, 490 тыс. руб.
Рассчитываем доверительный интервал прогноза.
