Лінійні диференціальні рівняння автоматичних систем і їх елементів

Найбільш спільною і найбільш повною формою математичного описання автоматичних систем і їх елементів є диференціальне рівняння. Але для більшості реальних елементів вихідне рівняння, складене строго у відповідності з законами фізики, є нелінійним. Ця обставина сильно ускладнює всі наступні процедури аналізу. Тому завжди прагнуть перейти від складнішого розв’язання нелінійного рівняння до лінійного диференціального рівняння

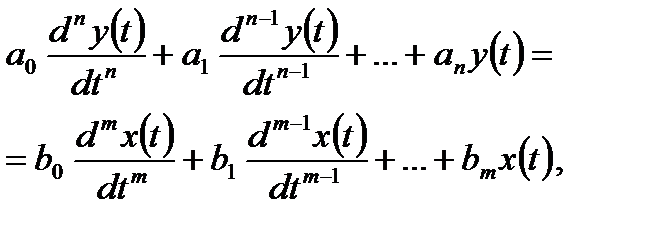(2.1)

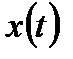де і 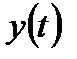– відповідно вхідна і вихідна величини елементу або системи; 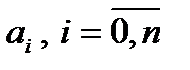, 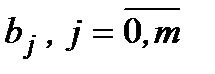– коефіцієнти рівняння.

Рівняння (2.1) встановлює зв’язок між вхідною величиною як в перехідних, так і в установлених режимах.

Коефіцієнти диференціального рівняння залежать від різних фізичних констант, що характеризують швидкість протікання процесів в елементах. Такими константами є, наприклад, маси частинок, що рухаються, індуктивності і ємності електронних ланцюгів, теплоємності нагрівальних елементів.

Інколи параметри деяких елементів систем змінюються в часі, причому швидкість їх зміни співставляється з швидкістю процесів управління в системі. Тоді систему називають нестаціонарною, або системою зі змінними параметрами. Системою зі змінними параметрами є, наприклад, автоматична система керування приводом повороту потужного екскаватора, якщо в процесі повороту одночасно виконується висування ручки з ковшом. В міру віддалення ковша від центра повороту платформи екскаватора сильно збільшується маховий момент маси навколо вертикальної осі і, отже, значно буде змінюватись один з коефіцієнтів диференціального рівняння.

В більшості практичних випадків коефіцієнти рівняння мало змінюються, і системи є системами з постійними параметрами. Далі будуть розглядатися тільки такі системи.

Якщо при складанні лінійного диференціального рівняння (2.1) використовуються лінеаризовані статичні характеристики або прийняті допущення про лінійності тих чи інших взаємозв’язків, то рівняння справедливе лише для малих відхилень вхідної і вихідної величин від їх значень в статичному режимі 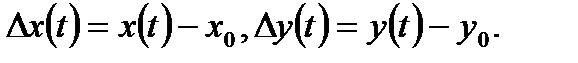Але для спрощення записів часто в лінійному рівнянні відхилення позначають тими ж символами (без знаку D), що й самі величини.

Для автоматичних систем керування, що описуються лінійним рівнянням (2.1), справедливий принцип накладання або суперпозиції, згідно з яким зміна вихідної величини 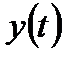, що виникає при дії на систему декількох вхідних сигналів, дорівнює сумі зміни величини 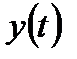, що викликаються кожним сигналом окремо. Ця властивість лінійних систем має практичне значення, так як, дякуючи йому, значно полегшує всі розрахунки.

Розглянемо тепер типові форми запису лінійного диференціального рівняння (2.1), які використовуються в різних задачах теорії автоматичного управління.

Як і в інших галузях науки і техніки, всі фізичні змінні, які входять в рівняння, можуть бути виражені у відносних одиницях. Для цього кожний доданок ділять на сталу величину, що має розмірність тієї змінної, яка входить в цей доданок. Сталі величини називають базовими. Як базові величини приймають переважно номінальні або встановлені значення змінних х і у.

Вигідною формою запису лінійних диференціальних рівнянь є символічна або операторна. Перехід до цієї форми здійснюється введенням скороченого умовного позначення операції диференціювання: 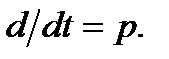Відповідно коефіцієнту похідну змінної у позначають

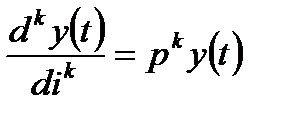, (2.2)

тоді рівняння (2.1) в символічній формі буде мати вигляд

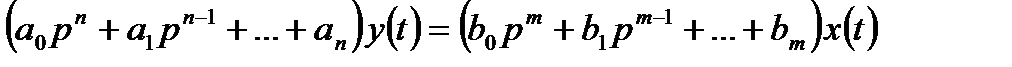. (2.3)

Многочлени від р степеня п і т, що знаходяться в лівій і правій частинах рівняння (2.3), називаються диференціальними операторами. Кожний такий оператор встановлює співвідношення між функцією часу і визначеною сукупністю похідних цієї функції. Многочлен

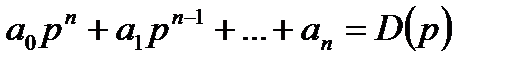(2.4)

називають власним оператором, а многочлен

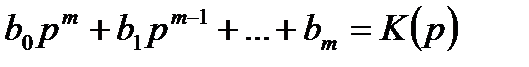(2.5)

– вхідним оператором або оператором дії.

Назва “власний” обумовлена тим, що многочлен 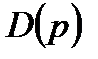характеризує власний рух елемента, рух за відсутності внутрішньої дії. Оператор 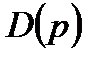називають також характеристичним.

У всіх реальних елементах і системах порядок найвищої похідної в вхідному операторі не може бути більшим від порядку найвищої похідної в власному операторі, тобто, всі 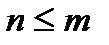. Якщо в процесі яких-небудь формальних викладок утворюється рівняння, в якому , то вважають, що це рівняння відповідає фізично нереалізуючій системі.

Рівняння елементів невисокого порядку (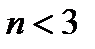) в теорії автоматичного управління прийнято записувати в так званій стандартній формі. При стандартній формі запису рівняння перетворюється таким чином, щоб коефіцієнт при вихідній величині був рівний одиниці. При цьому коефіцієнт перед вхідною величиною в правій частині рівняння стає рівним передавальному коефіцієнту, а коефіцієнти при похідних вихідної величини будуть мати розмірність часу в степені, рівній порядку відповідної похідної. Наприклад, рівняння другого порядку

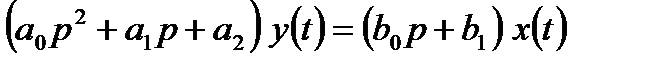(2.6)

шляхом ділення всіх членів на коефіцієнт може бути приведене до стандартної форми

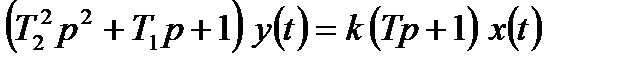, (2.7)

де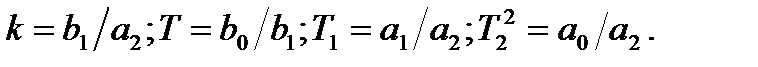

Коефіцієнти 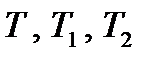називають сталими часу. Вони характеризують динамічні властивості елемента. Часто при дослідженні автоматичних систем виявляється вигідним перехід від природного часу t, виміряного в секундах, хвилинах, до так званого безрозмірного (відносного) часу 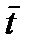. Цей перехід здійснюють за допомогою деякого сталого (в загальному випадку – довільно вибраного) множника , який має розмірність часу.

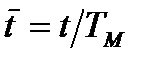. (2.8)

Як множник часто беруть сталу часу одного з елементів, що входять в систему. Величину, обернену до множника , називають масштабом часу і позначають .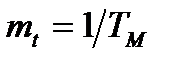

Оператор k-кратного диференціювання за безрозмірним часом зв’язаний із звичайним оператором диференціювання 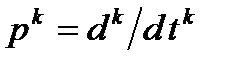співвідношенням

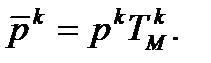(2.9)

Використовуючи співвідношення (2.9), можна будь-яке диференціальне рівняння записати в безрозмірному часі, який вимірюється в умовних одиницях . Наприклад, рівняння (2.6) буде мати вигляд

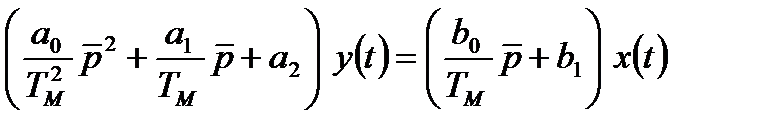. (2.10)

Якщо коефіцієнт перетворення часу вибирають за визначеним правилом, а саме:

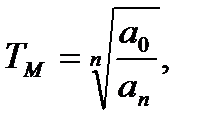(2.11)

то можна максимально спростити диференціальне рівняння. Так, рівняння (2.10) набуде вигляду

, (2.12)

де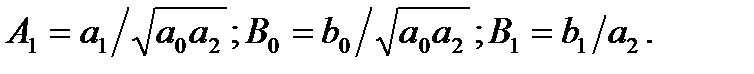

В лівій частині рівняння замість трьох числових коефіцієнтів 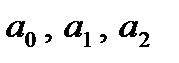залишився лише один коефіцієнт 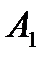. Така компактна форма запису була вперше використана І.А.Вишнеградським (для рівняння 3-го порядку) і називається формою Вишнеградського.

Важливою перевагою цієї форми є те, що введення безрозмірного часу 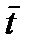в диференціальне рівняння не впливає на характер функції 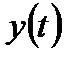(міняється тільки масштаб незалежної змінної t). Тому заміна масштабу часу широко використовується при дослідженні автоматичних систем на аналогових обчислювальних машинах. При цьому приходять як до “приско-рення” часу (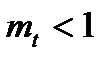), так і до “сповільнення” часу ().

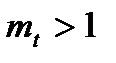Заміна масштабу часу полегшує в багатьох випадках аналіз динаміки автоматичних систем, дозволяє одержати результати в найбільш загальному, універсальному вигляді.

Приклад. Складемо і запишемо в типових формах диференціальне рівняння механічної частини виконуючого пристрою, зображеного на рис. 2.1. Сила 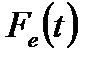, утворена електромагнітом і прикладена в точці 3, через важіль передається на виконавчий орган – заслінку. Вихідною величиною слід вважати переміщення заслінки 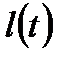, так як від величини переміщення залежать пропускна здатність трубопроводу і режим роботи всього наступного ланцюжка елементів автоматичної системи. (Зазначимо, що нерідко призначення електромагніта – створення тиску на об’єкт, і тоді як вихідну величину слід розглядати силу).

Згідно з відомим законом механіки – принципом Даламбера – сума всіх моментів, діючих на важіль, повинна дорівнювати нулю

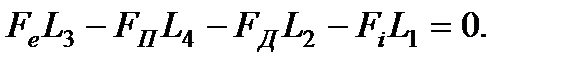(2.13)

Так як кут повороту важеля змінюється в невеликих межах, то замість обертового руху можна розглядати поступальний, а рівняння руху записати для лінійного переміщення однієї з точок важеля (наприклад, для точки 1). Відповідно всі сили і маси необхідно привести в дану точку. Тоді замість рівняння моментів (2.13) можна записати рівняння сил, приведених в точку 1

(2.14)

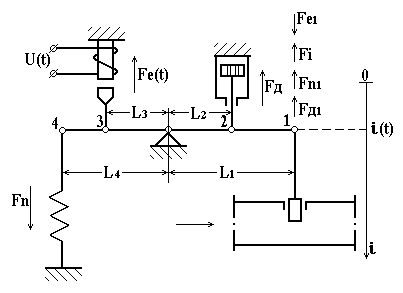Рисунок 2.1 – Конструктивна схема електромагнітного виконавчого пристрою

Сила інерції 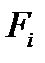пропорційна прискоренню в точці 1 і масі пересувних частинок пристрою

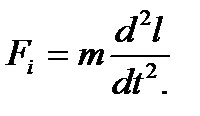, (2.15)

де т – сума мас, приведених в точку 1, кг.

Силу демпфера 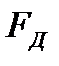з достатньою для практичних розрахунків точністю можна вважати пропорційною швидкості переміщення точки 2

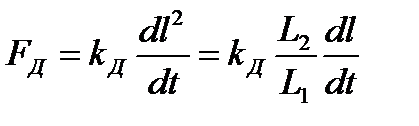, (2.16)

де 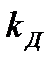– коефіцієнт демпфування, що залежить від конструктивних параметрів демпфера (площі поршня і діаметра дірок в ньому), Н/(м/с).

Сила пружності пружини 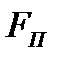пропорційна величині переміщення точки 4

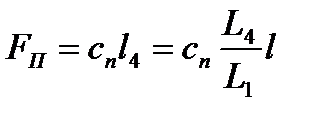, (2.17)

де 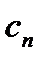– коефіцієнт пружності (жорсткості) пружини, Н/м.

Підставляючи вирази (2.15), (2.16), (2.17) у рівняння сил (2.14), одержимо диференціальне рівняння, котре зв’язує вхідну і вихідну величини механічної частини пристрою

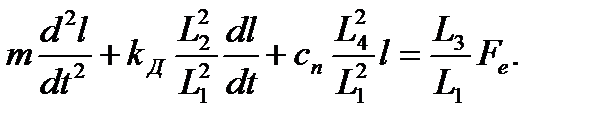(2.18)

Після ділення лівої і правої частини рівняння (2.18) на величину 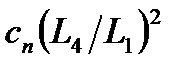його можна записати в стандартній формі

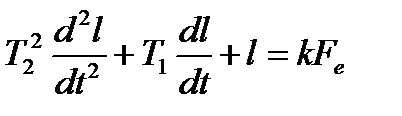, (2.19)

де 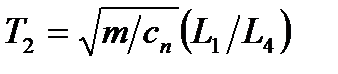– стала часу, яка характеризує коливальні властивості пристрою, с; 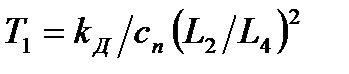– стала часу, яка характеризує демпфуючі властивості, с; 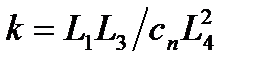– передавальний коефіцієнт пристрою, що залежить від пружності пружини і співвідношення плечей руки, м/Н.

При складанні рівняння (2.19) було прийнято, що сила тертя пропорційна швидкості переміщення і що ліве і праве плечі ручки не доходять до відказу. Обидва ці передбачення справедливі лише при обмеженому діапазоні зміни величин 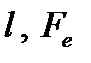і їх похідних. Тому, хоч лінеаризація в явному вигляді і не здійснюється, рівняння (2.19) є в дійсності лінеаризованим і, отже, справджується лише для відхилень Dl і DF_e вказаних величин від значень, котрі відповідають точкам лінеаризації або серединам діапазонів, які розглядаємо.

Запишемо тепер рівняння (2.19) у відносних одиницях. Для цього приймемо як базові значення змінних 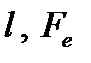деякі сталі величини і 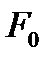і введемо позначення 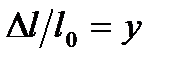і 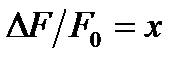. Тоді рівняння (2.19) після нескладних перетворень набуде вигляду

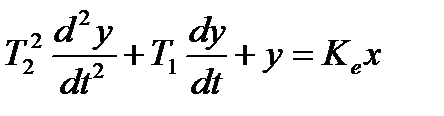, (2.20)

де 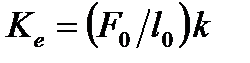– безмежний передавальний коефіцієнт приладу.

Для того, щоб записати рівняння в безмежному часі, візьмемо за одиницю часу одну з сталих часу приладу, наприклад, величину 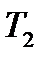. Тоді час, який вимірюється в одиницях ,

,

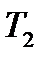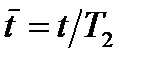відповідно

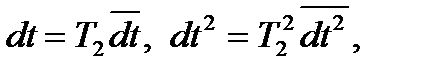
диференціальне рівняння (2.20) матиме вигляд

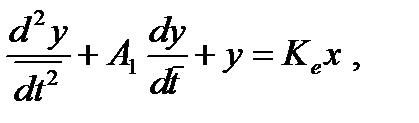(2.21)

де 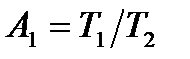– безрозмірний коефіцієнт рівняння.