
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типові алгоритмічні ланки, їх частотні та часові характеристики
|
|
3.1 Поняття алгоритмічної, типової і елементарної ланок
Багато технічних наук використовують умовні поняття для вирішення науково-технічних задач. Наприклад, в електротехніці користуються R, L, C і з їх допомогою проводять розрахунок електричних ланцюгів.
Аналогічно і в ТАК: систему керування можна синтезувати на основі типових динамічних ланок. Для цього використовують знання вищої математики, а саме: перетворення Лапласа, Фур’є та інші.
При вивченні роботи автоматичних систем ми класифікували елементи за функціональними ознаками. Це давало можливість вивчити взаємодію керованого об’єкта з керуючим пристроєм, а також їх елементів. Можна класифікувати елементи за динамічними властивостями. Така класифікація спрощує розв’язок задач аналізу. Виявляється, що незважаючи на розмірність елементів, багато з них мають однакові динамічні властивості.
Наприклад, двигуни постійного і змінного струмів після їх включення набирають швидкість за таким законом, за яким проходить зміна струму в їх обмотках. Всі ці процеси описуються диференціальними рівняннями першого порядку. В цьому проявляється єдність природи.
Загальність математичних виразів, що зв’язують вхідні і вихідні величини різних елементів, дозволяють виділити обмежену кількість типових алгоритмічних ланок.
Кожному типу алгоритмічної ланки відповідає математичне співвідношення між вхідною і вихідною величинами. Якщо ці співвідношення є елементарними, то такі алгоритмічні ланки називають елементарними.
Алгоритмічні ланки, які описуються звичайними диференціальними рівняннями І-го і ІІ-го порядку, називаються типовими динамічними ланками.
Типові динамічні ланки – це ланки спрямованої дії. Сигнали передаються тільки з входу на вихід. При зміні вхідного сигналу повинен змінюватись вихідний сигнал. Причому, якщо ланки з’єднані між собою, то наступна ланка не повинна впливати на попередню. Але ця вимога виконується не завжди.
При створенні класифікації динамічних ланок виникає проблема – скільки повинно бути ланок? Ця задача вирішена в 1938 році Михайловим. Він довів, що класифікація типових динамічних ланок може бути виконана на основі диференціального рівняння ІІ-го порядку:
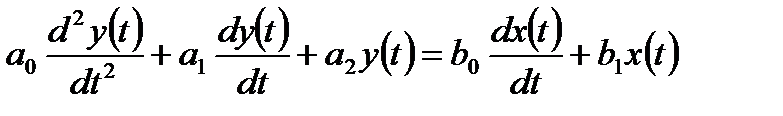 . (3.1)
. (3.1)
З цього рівняння можна отримати 12 рівнянь шляхом зміни коефіцієнтів 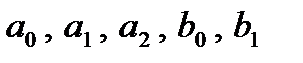 (табл. 3.3).
(табл. 3.3).
Аналіз великої кількості елементів системи автоматичного керування вказує, що більшість з них мають динамічні властивості, які можна описати диференціальними рівняннями другого порядку.
Ланки, в яких 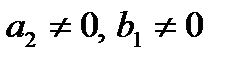 , мають властивості статизму, тобто однозначний зв’язок між входом і виходом в статичному режимі. Тому її називають статичними або позиційними. До них відносяться 1, 2, 3, 4, 10, 11, 12. Ланки, в яких
, мають властивості статизму, тобто однозначний зв’язок між входом і виходом в статичному режимі. Тому її називають статичними або позиційними. До них відносяться 1, 2, 3, 4, 10, 11, 12. Ланки, в яких 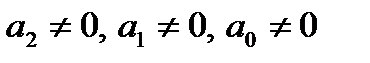 , мають властивості інерційності (2, 3, 4, 6, 8, 11, 12). Ланки 1, 5, 7 мають два коефіцієнти, які не дорівнюють нулю – ці ланки називають елементарними. Всі інші ланки можуть бути створені з елементів шляхом послідовного, паралельного, зустрічно-паралельного з’єднань.
, мають властивості інерційності (2, 3, 4, 6, 8, 11, 12). Ланки 1, 5, 7 мають два коефіцієнти, які не дорівнюють нулю – ці ланки називають елементарними. Всі інші ланки можуть бути створені з елементів шляхом послідовного, паралельного, зустрічно-паралельного з’єднань.
В диференціальному рівнянні ІІ-го порядку, яке розглядається, всі коефіцієнти додатні. Виникає проблема – як зміняться властивості елементів, якщо хоч би один із коефіцієнтів диференціального рівняння від’ємний. Відповідь можна отримати, розглянувши хоча б одне диференціальне рівняння І-го порядку
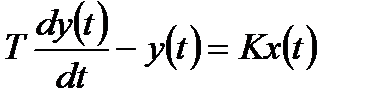 .
.
Перетворимо його за Лапласом
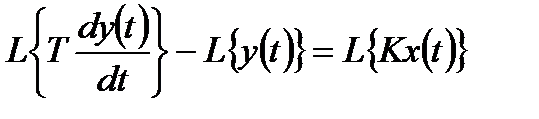 ,
,
 ,
, 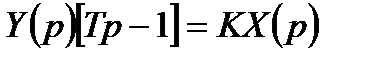 ,
,
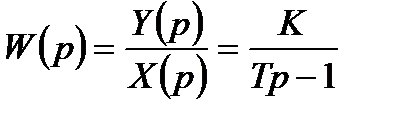 .
.
Щоб знайти перехідні характеристики, потрібно взяти зворотне перетворення за Лапласом
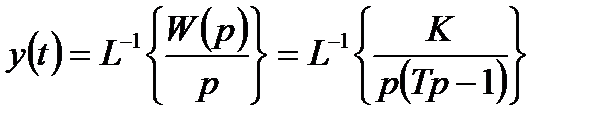 .
.
Тоді 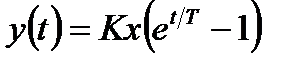 .
.
Побудувавши графік 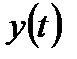 (рис. 3.1), бачимо, що така ланка нестійка.
(рис. 3.1), бачимо, що така ланка нестійка.
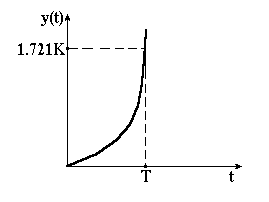 Рисунок 3.1 – Перехідна характеристика нестійкої ланки 1-го порядку
Рисунок 3.1 – Перехідна характеристика нестійкої ланки 1-го порядку
|