
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгебраїчні критерії стійкості
|
|
Перший алгебраїчний критерій, який можна використовувати для системи 3-го порядку, був сформульований І.А.Вишнеградським в 1876 р.:
для стійкості лінійної системи з характеристичним рівнянням

необхідне виконання двох умов:
1) всі коефіцієнти характеристичного рівняння повинні бути додатними;
2) похідна середніх коефіцієнтів повинна бути більша від похідної крайніх
 .
.
В коефіцієнти рівнянь входять лише значення параметрів системи, тому стійкість останньої визначається тільки параметрами і не залежить від їх стану.
Для визначення систем будь-якого типу порядку використовують критерії Гурвіца та Рауса. Критерій Гурвіца більш простіший, тому його використовують частіше. Він формулюється так:
Система з характеристичним рівнянням
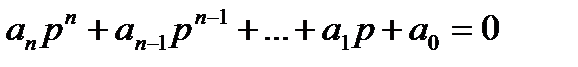
буде стійкою, якщо визначник і всі його діагональні мінори додатні:
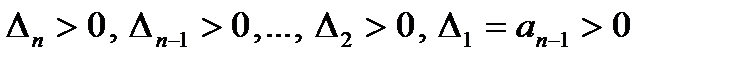 .
.
При складанні визначника Гурвіца спочатку по діагоналі розміщують коефіцієнти, починаючи з 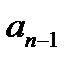 до
до 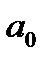 :
:
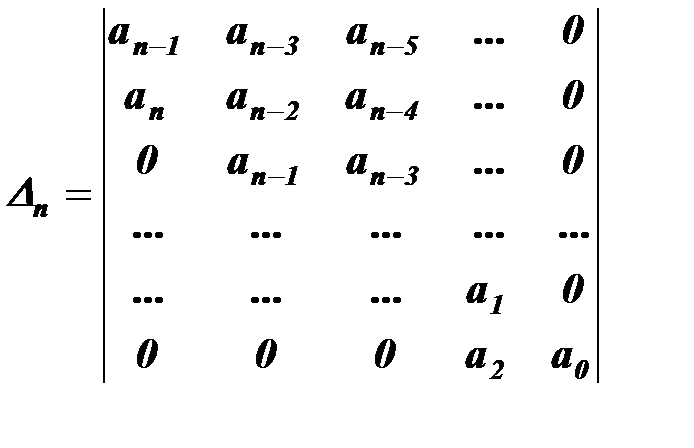 . (4.8)
. (4.8)
Потім визначник заповнюють по стовпцях: вище діагональних коефіцієнтів записуються коефіцієнти із індексами, що зменшуються, а нижче – із зростаючими. При досягненні нульового або n-го індексу далі ставляться нулі.
Кожен діагональний мінор 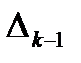 визначника Гурвіца отримують з попереднього мінору
визначника Гурвіца отримують з попереднього мінору 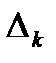 шляхом викреслювання нижнього рядка і правого стовпчика. Мінор
шляхом викреслювання нижнього рядка і правого стовпчика. Мінор 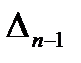 отримують з визначника Гурвіца
отримують з визначника Гурвіца 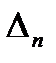 за загальним правилом, тобто шляхом викреслювання з
за загальним правилом, тобто шляхом викреслювання з 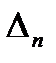 нижнього рядка і правого стовпчика. Нижчий діагональний мінор Гурвіца
нижнього рядка і правого стовпчика. Нижчий діагональний мінор Гурвіца 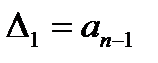 .
.
Як приклад використаємо критерій Гурвіца для визначення стійкості системи з характеристичним рівнянням
 .
.
Складемо визначник Гурвіца і його діагональні мінори
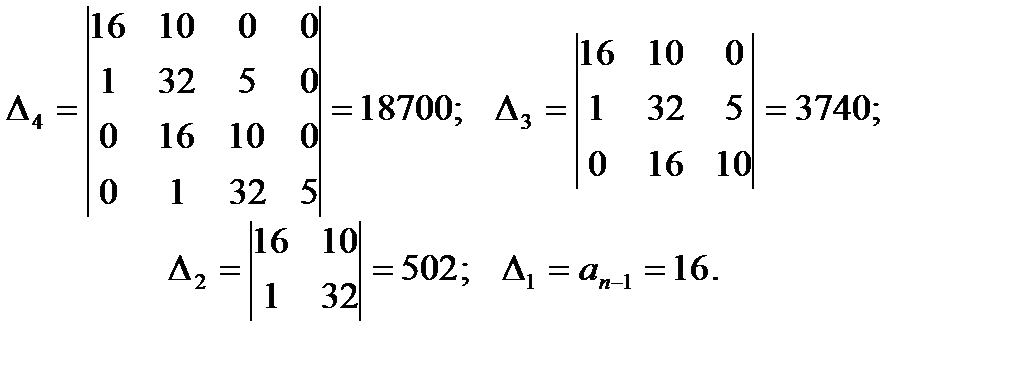
Звідси видно, що визначник Гурвіца і його діагональні мінори додатні. Отже, система, що досліджується, стійка.
Позитивною ознакою алгебраїчних критеріїв є простота використання, а недоліком – те, що вони не дозволяють оцінити вплив на стійкість системи параметрів окремих її елементів. Цього недоліку можна позбутися за допомогою графоаналітичного критерію А.В.Михайлова.