
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 1. Даны вершины треугольника АВС.
|
|
Даны вершины треугольника АВС.
Найти: а) длину стороны АВ; б) уравнения сторон АВ и АС и их угловые коэффициенты; в) внутренний угол А в радианах с точностью до 0, 01; г) уравнение высоты СD и ее длину; д) уравнение окружности, для которой высота СD есть диаметр.
1. А(–5; 0), В(7; 9), С(5; –5).
2. А(–7; 2), В(5; 11), С(3; –3).
3. А(–5; –3), В(7; 6), С(5; –8).
4. А(–6; –2), В(6; 7), С(4; –7).
5. А(–8; –4), В(4; 5), С(2; –9).
6. А(0; –1), В(12; 8), С(10; –6).
7. А(–6; 1), В(6; 10), С(4; –4).
8. А(–2; –4), В(10; 5), С(8; –9).
9. А(–3; 0), В(9; 9), С(7; –5).
10. А(–9; –2), В(3; 7), С(1; –7).
Задача 2.
Составить уравнение линии, для каждой точки которой отношение расстояний до точки А (х 1; у 1) и до прямой 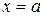 равно числу ε. Полученное уравнение привести к простейшему виду и построить кривую.
равно числу ε. Полученное уравнение привести к простейшему виду и построить кривую.
1. А (4; 0), а = 9, 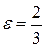 .
.
2. А (–8; 0), а = –2, 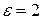 .
.
3. А (4; 0), а = 1, 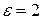 .
.
4. А (9; 0), а = 4, 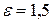 .
.
5. А (–1; 0), а = –4, 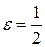 .
.
Составить уравнение линии, для каждой точки которой ее расстояние до точки А (х 1; у 1) равно расстоянию до прямой 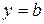 . Полученное уравнение привести к простейшему виду и построить кривую.
. Полученное уравнение привести к простейшему виду и построить кривую.
6. А (2; 1), b = –1.
7. А (–2; –2), b = –4.
8. А (2; –1), b = 2.
9. А (2; –1), b = 1.
10. А (4; –1), b = 1.