
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Матрицы, операции над ними
|
|
1. Матрицей размера m ´ n называется прямоугольная таблица чисел, содержащая m строк и n столбцов.
Числа, составляющие матрицу, будем называть элементами матрицы аij, где i – номер строки, j – номер столбца или, в сокращенной записи, А =(аij); i = 1, 2, …, m; j = 1, 2, …, n.
Виды матриц
1) Матрица, состоящая из одной строки, называется матрицей-строкой (вектором-строкой), а из одного столбца – матрицей-столбцом (вектором-столбцом):
А = (а11; а12, …, а1n) – матрица-строка;

 1´ n
1´ n
b11
В = b21 – матрица-столбец
… m ´ 1
bm1
2) Матрица называется квадратной, если число ее строк равно числу столбцов.
3) Квадратная матрица А называется невырожденной, если 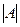
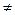 0.
0.
4) Квадратная матрица называется диагональной, если все ее недиагональные элементы равны нулю.
5) Диагональная матрица называется единичной, если все диагональные элементы равны единице, и обозначается Е.
6) Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю, и обозначается (0).
7) Матрица А называется треугольной (ступенчатой, если m 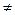 n), если ниже ее главной диагонали все элементы равны нулю.
n), если ниже ее главной диагонали все элементы равны нулю.
Операции над матрицами
|
где i = 1, 2, …, m; j = 1, 2, …, n.
2. Суммой двух матриц А и В одинакового размера m ´ n называется матрица С, элементы которой cij = аij+ bij, т.е.
|
где i = 1, 2, …, m; j = 1, 2, …, n,
причем А+В = В+А; (А+В)+С = А+(В+С); l(А+В) = lА+lВ.
3. Разность двух матриц одинакового размера определяется через предыдущие операции: А – В = А + (–1)· В
4. Произведением матрицы А размера (m ´ k) на матрицу В размера (k ´ n) называется матрица С размера (m ´ n), элемент которой
сij = 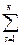 аisbsj, для i = 1, 2, …, m; j = 1, 2, …, n; т.е.
аisbsj, для i = 1, 2, …, m; j = 1, 2, …, n; т.е.
|
Свойства умножения матриц
1) А·В 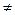 В·А – (в общем случае)
В·А – (в общем случае)
2) (А·В)·С = А·(В·С) – сочетательный закон.
3) l (А·В) = (lА) В = А·(lВ)
4) А·(В+С) = А·В + А·С
5) А·Е = Е·А = А,
где Е – единичная матрица того же размера, что и матрица А.





 6) Если С = А·В, то С = А· В, где А и В квадратные матрицы.
6) Если С = А·В, то С = А· В, где А и В квадратные матрицы.
5. Целой положительной степенью Аm (m > 1) квадратной матрицы А называется произведение m матриц, равных А, т.е. Аm = А·А·…·А
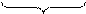
m раз
6. Транспонирование матрицы – переход от матрицы А к матрице АТ, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица АТ называется транспонированной относительно матрицы А.
7. Матрица А -1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица, т.е. А -1 ·А = А·А -1 = Е.
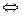 bij = l аij,
bij = l аij,