
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 3. В задачах 1–10 даны координаты точек А, В, С
|
|
В задачах 1–10 даны координаты точек А, В, С. Требуется: а) записать векторы 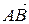 и
и 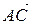 и найти модули этих векторов; б) найти угол между векторами
и найти модули этих векторов; б) найти угол между векторами 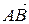 и
и 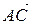 ; в) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору
; в) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору 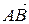 и изобразить ее на чертеже, используя уравнение плоскости «в отрезках».
и изобразить ее на чертеже, используя уравнение плоскости «в отрезках».
1. А(7; –4; 1), В(12; –3; 1), С(10; 1; 5).
2. А(0; –3; 3), В(5; –2; 3), С(3; 2; 7).
3. А(–2; –1; –2), В(3; 0; –2), С(1; 4; 2).
4. А(–6; 0; 0), В(–1; 1; 0), С(–3; 5; 4).
5. А(–2; –3; –8), В(3; –2; –8), С(1; 2; –4).
6. А(1; 0; –1), В(6; 1; –1), С(4; 5; 3).
7. А(–1; 4; 1), В(4; 5; 1), С(2; 9; 5).
8. А(3; –6; –3), В(8; –5; –3), С(6; –1; 1).
9. А(1; 0; 0), В(6; 1; 0), С(4; 5; 4).
10. А(2; –8; –2), В(7; –7; –2), С(5; –3; 2).
Задача 4.
Систему уравнений записать в матричной форме и решить: а) с помощью обратной матрицы, б) с помощью правила Крамера и в) методом Гаусса.
1. 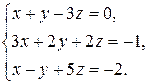 2.
2. 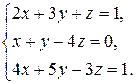
3. 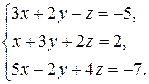 4.
4. 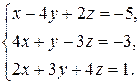
5. 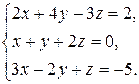 6.
6. 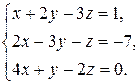
7. 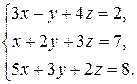 8.
8. 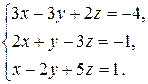
9. 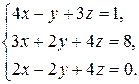 10.
10. 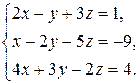
Задача 5.
Найти указанные пределы.
1. а) 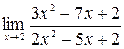 ; б)
; б) 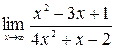 ;
;
в) 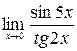 ; г)
; г) 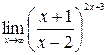 .
.
2. а) 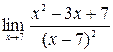 ; б)
; б) 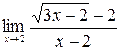 ;
;
в) 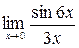 ; г)
; г) 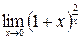 .
.
3. а) 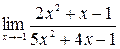 ; б)
; б) 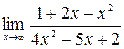 ;
;
в) 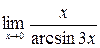 ; г)
; г) 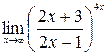 .
.
4. а) 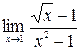 ; б)
; б) 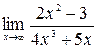 ;
;
в) 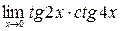 ; г)
; г) 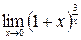 .
.
5. а) 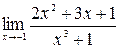 ; б)
; б)  ;
;
в) 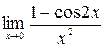 ; г)
; г) 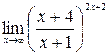 .
.
6. а) 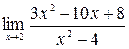 ; б)
; б) 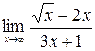 ;
;
в) 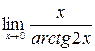 ; г)
; г) 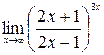 .
.
7. а) 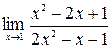 ; б)
; б) 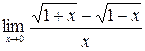 ;
;
в) 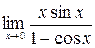 ; г)
; г) 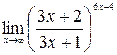 .
.
8. а) 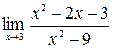 ; б)
; б) 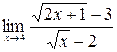 ;
;
в)  ; г)
; г) 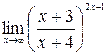 .
.
9. а) 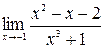 ; б)
; б) 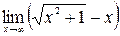 ;
;
в) 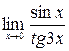 ; г)
; г) 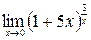 .
.
10. а) 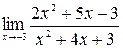 ; б)
; б) 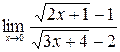 ;
;
в) 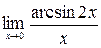 ; г)
; г) 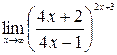 .
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
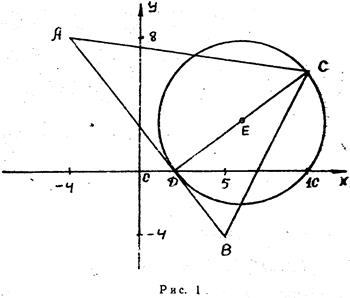
Задача 1. Даны вершины треугольника АВС: А(–4; 8), В(5; –4), С(10; 6).
Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0, 01; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр.
Решение.
1. Расстояние 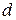 между точками
между точками 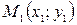 и
и 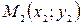 определяется по формуле:
определяется по формуле:
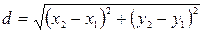 . (1)
. (1)
Подставив в эту формулу координаты точек А и В, имеем:
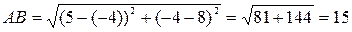 .
.
2. Уравнение прямой, проходящей через точки 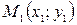 и
и 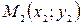 , имеет вид:
, имеет вид:
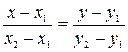 . (2)
. (2)
Подставив в (2) координаты точек:
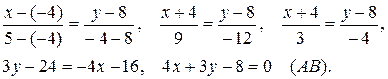
Для нахождение углового коэффициента 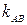 прямой АВ разрешим полученное уравнение относительно у:
прямой АВ разрешим полученное уравнение относительно у: 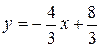 . Отсюда
. Отсюда 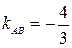 . Подставив в формулу (2) координаты точек А и С, получим уравнение прямой АС.
. Подставив в формулу (2) координаты точек А и С, получим уравнение прямой АС.
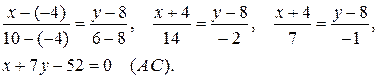
Отсюда 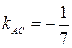 .
.
3. Угол 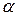 между двумя прямыми, угловые коэффициенты которых равны
между двумя прямыми, угловые коэффициенты которых равны 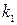 и
и 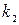 , определяется по формуле:
, определяется по формуле:
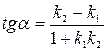 . (3)
. (3)
Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее 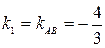 ,
, 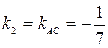 .
.
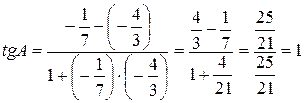 ,
,
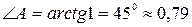 рад.
рад.
4. Так как высота 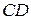 перпендикулярна стороне
перпендикулярна стороне 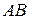 , то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.
, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.
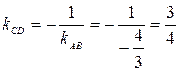 .
.
Уравнение прямой, проходящей через данную точку 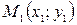 в заданном угловым коэффициентом
в заданном угловым коэффициентом 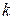 направлении, имеет вид:
направлении, имеет вид:
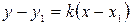 . (4)
. (4)
Подставив в (4) координаты точки С и 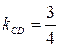 , получим уравнение высоты
, получим уравнение высоты 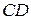 :
:
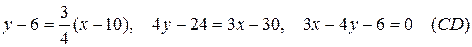 . (5)
. (5)
Для нахождения длины 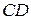 определим координаты точки
определим координаты точки 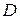 , решив систему уравнений (АВ) и (
, решив систему уравнений (АВ) и (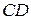 ):
):
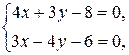
откуда 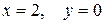 , то есть
, то есть 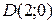 .
.
Подставив в формулу (1) координаты точек С и 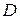 , находим:
, находим:
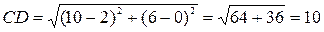 .
.
5. Уравнение окружности радиуса 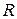 с центром в точке
с центром в точке 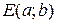 имеет вид:
имеет вид:
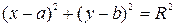 . (6)
. (6)
Так как 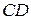 является диметром искомой окружности, то ее центр Е есть середина отрезка
является диметром искомой окружности, то ее центр Е есть середина отрезка 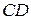 . Воспользовавшись формулами деления отрезка пополам, получим:
. Воспользовавшись формулами деления отрезка пополам, получим:
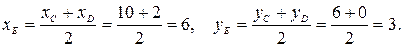
Следовательно, 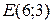 и
и 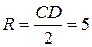 . Используя формулу (6), получаем уравнение искомой окружности:
. Используя формулу (6), получаем уравнение искомой окружности:
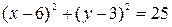 .
.
На рис. 1 в декартовой прямоугольной системе координат 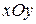 изображен треугольник
изображен треугольник 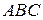 , высота
, высота 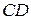 , окружность с центром в точке Е.
, окружность с центром в точке Е.
Задача 2. Составить уравнение линии, для каждой точки которой отношение расстояний до точки 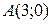 и до прямой
и до прямой 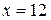 равно числу
равно числу 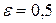 . Полученное уравнение привести к простейшему виду и построить кривую.
. Полученное уравнение привести к простейшему виду и построить кривую.
Решение.
Пусть 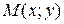 – текущая (произвольная) точка искомого геометрического множества точек. Опустим перпендикуляр
– текущая (произвольная) точка искомого геометрического множества точек. Опустим перпендикуляр 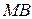 на прямую
на прямую 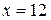 (рис. 2). Тогда
(рис. 2). Тогда 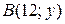 . По условию задачи
. По условию задачи 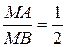 . По формуле (1) из предыдущей задачи
. По формуле (1) из предыдущей задачи
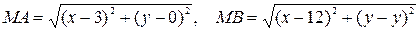 .
.
Тогда
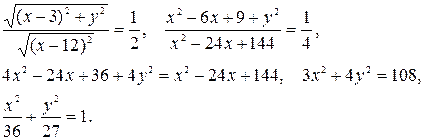
Полученное уравнение представляет собой эллипс вида 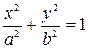 , где
, где 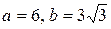 .
.
Определим фокусы эллипса 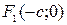 и
и 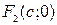 . Для эллипса справедливо равенство
. Для эллипса справедливо равенство 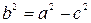 , откуда
, откуда 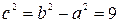 и
и 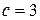 . То есть
. То есть 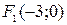 и
и 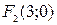 – фокусы эллипса (точки
– фокусы эллипса (точки 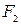 и А совпадают).
и А совпадают).
Эксцентриситет эллипса 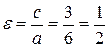 .
.
 у
у
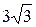 М В
М В

F 1 А
-6 –3 0 3 6 12 х
Рис. 2
Задача 3. Составить уравнение геометрического места точек, отношение расстояний которых до точки 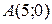 и до прямой
и до прямой 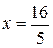 равно числу
равно числу 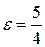 .
.
Решение.
Пусть 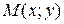 – произвольная точка искомого геометрического множества точек. Опустим перпендикуляр
– произвольная точка искомого геометрического множества точек. Опустим перпендикуляр 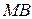 на прямую
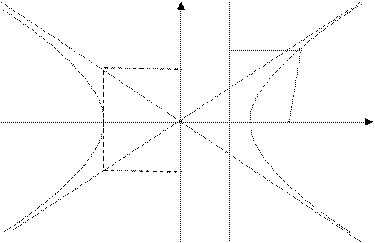
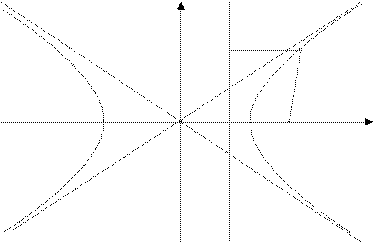
на прямую 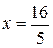 и определим координаты точки В (рис. 3). Очевидно, что абсцисса точки
и определим координаты точки В (рис. 3). Очевидно, что абсцисса точки 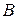 равна
равна 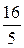 (так как точка В лежит на прямой
(так как точка В лежит на прямой 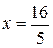 ), а ордината точки В равна ординате точки М. Следовательно, имеем:
), а ордината точки В равна ординате точки М. Следовательно, имеем: 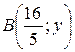 .
.
 у
у
3 В М
 |
–4 0 4 А х
-3
Рис. 3
По условию задачи 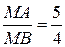 ; так как
; так как
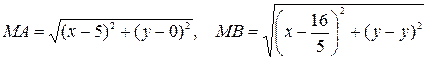 , то получаем:
, то получаем:
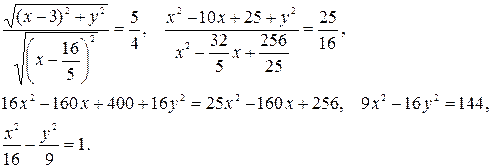
Полученное уравнение представляет собой гиперболу вида 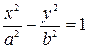 , где
, где 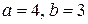 .
.
Задача 4. Составить уравнение линии, для каждой точки которой ее расстояние до точки 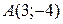 равно расстоянию до прямой
равно расстоянию до прямой 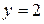 . Полученное уравнение привести к простейшему виду и построить кривую.
. Полученное уравнение привести к простейшему виду и построить кривую.
Решение.
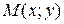 – текущая точка искомой кривой. Опустим из точки М перпендикуляр МВ на прямую
– текущая точка искомой кривой. Опустим из точки М перпендикуляр МВ на прямую 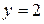 (рис. 4). Тогда
(рис. 4). Тогда 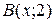 . Так как
. Так как 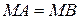 , то
, то
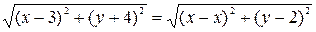 или
или
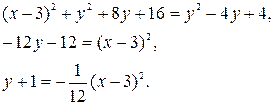
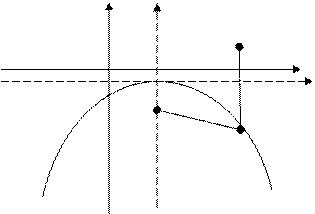 y У’
y У’
2 B

0 3 х
Х’
–4 А
M
Рис. 4
Полученное уравнение определяет параболу с вершиной в точке 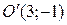 . Для приведения уравнения параболы к простейшему (каноническому) виду положим
. Для приведения уравнения параболы к простейшему (каноническому) виду положим 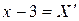 ,
, 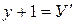 . Тогда в системе координат
. Тогда в системе координат 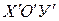 уравнение параболы принимает следующий вид:
уравнение параболы принимает следующий вид: 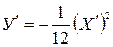 . В системе координат
. В системе координат 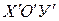 строим параболу.
строим параболу.
Задача 5. Даны координаты трех точек:
А (3; 0; –5), В (6; 2; 1), С (12; –12; 3).
Требуется: 1) записать векторы 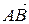 и
и 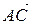 в системе орт и найти модули этих векторов; 2) найти угол между векторами
в системе орт и найти модули этих векторов; 2) найти угол между векторами 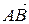 и
и 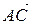 ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору
; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору 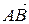 .
.
Решение.
1) Если даны точки 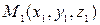 и
и 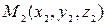 , то вектор
, то вектор 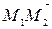 через орты
через орты 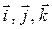 выражается следующим образом:
выражается следующим образом:
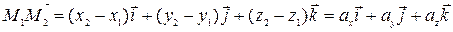 .
.
Подставляя в эту формулу координаты точек А и В, имеем:
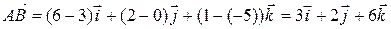 .
.
Аналогично
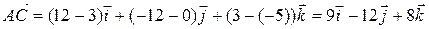 .
.
Модуль вектора 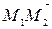 вычисляется по формуле
вычисляется по формуле
 .
.
Подставляя в формулу найденные ранее координаты векторов 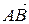 и
и 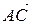 , находим их модули:
, находим их модули:
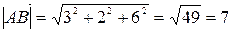 ,
,
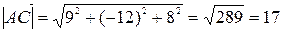 .
.
2) Косинус угла 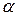 , образованного векторами
, образованного векторами 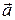 и
и 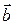 , равен их скалярному произведению, деленному на произведение их модулей
, равен их скалярному произведению, деленному на произведение их модулей
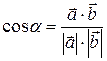 .
.
Так как скалярное произведение двух векторов, заданных своими координатами, равно сумме попарных произведений одноименных координат, то
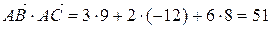 .
.
Тогда
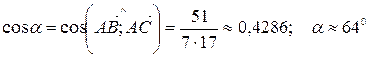 .
.
3) Уравнение плоскости, проходящей через точку 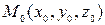 перпендикулярно вектору
перпендикулярно вектору 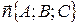 , имеет вид
, имеет вид
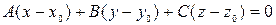 .
.
По условию задачи искомая плоскость проходит через точку 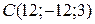 перпендикулярно вектору
перпендикулярно вектору 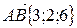 . Подставляя
. Подставляя 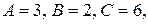
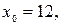
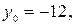
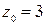 , получим:
, получим:
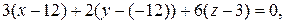
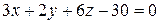 – искомое уравнение плоскости.
– искомое уравнение плоскости.
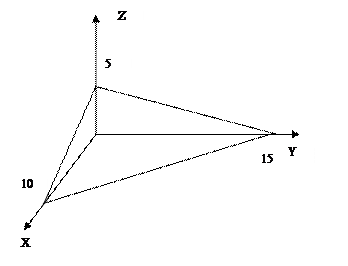
Перенеся свободный член -30 в правую часть тождества и разделив на 30 все члены выражения, получим уравнение плоскости «в отрезках»:
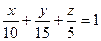 .
.
Строим чертеж.
Задача 6, а. Данную систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы:
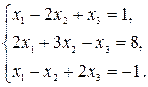
Решение.
Обозначим через А – матрицу коэффициентов при неизвестных; Х – матрицу-столбец неизвестных 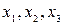 ; Н – матрицу-столбец свободных членов:
; Н – матрицу-столбец свободных членов:
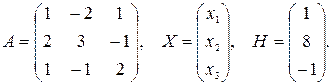
С учетом этих обозначений данная система уравнений принимает следующую матричную форму:
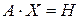 . (1)
. (1)
Если матрица А – невырожденная (ее определитель 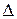 отличен от нуля), то она имеет обратную матрицу
отличен от нуля), то она имеет обратную матрицу 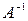 . Умножив обе части уравнения (1) на
. Умножив обе части уравнения (1) на 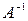 , получим:
, получим:
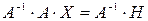 . (2)
. (2)
Но 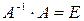 (Е – единичная матрица), а
(Е – единичная матрица), а 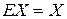 , поэтому
, поэтому
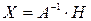 .
.
Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу 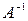 .
.
Пусть имеем невырожденную матрицу
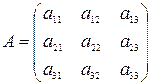 . Тогда
. Тогда 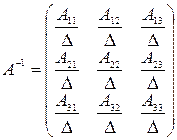 ,
,
где 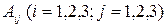 – алгебраическое дополнение элемента
– алгебраическое дополнение элемента 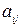 в определителе матрицы А, которое является произведением
в определителе матрицы А, которое является произведением 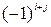 на минор (определитель) второго порядка, полученный вычеркиванием
на минор (определитель) второго порядка, полученный вычеркиванием 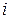 -ой строки и
-ой строки и 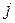 -го столбца в определителе матрицы А.
-го столбца в определителе матрицы А.
Вычислим определитель 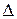 и алгебраические дополнения
и алгебраические дополнения 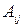 элементов матрицы А.
элементов матрицы А.
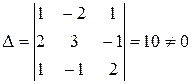 – следовательно матрица А имеет обратную матрицу
– следовательно матрица А имеет обратную матрицу 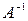 .
.
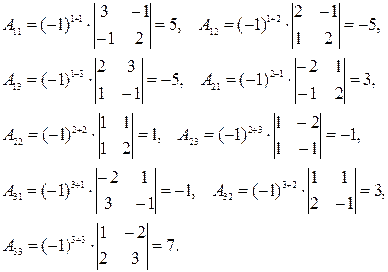
Тогда 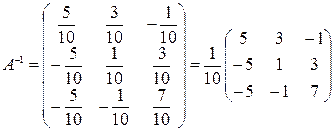 .
.
По формуле (2) находим решение данной системы уравнений в матричной форме:
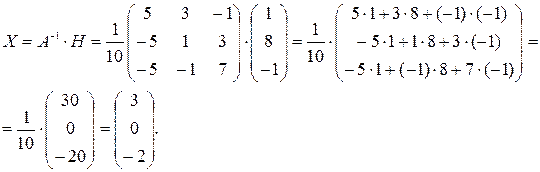
Откуда получаем решение 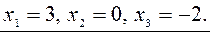
Задача 6, б. Решить систему по формулам Крамера
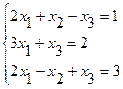
Решение.
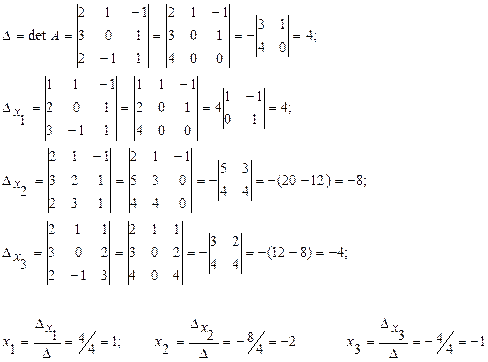
Задача 6, в. Решить систему линейных уравнений методом Гаусса, выполнить проверку: 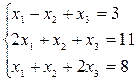 . (2)
. (2)
Решение.
Составим расширенную матрицу и выполним над ней элементарные преобразования, указанные в методе Гаусса.
Метод Гаусса решения системы (2) состоит в следующем:
Разделим все члены первого уравнения на 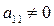 , а затем, умножив полученное уравнение на
, а затем, умножив полученное уравнение на 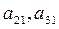 , вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное
, вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное 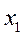 будет исключено, и получится система вида:
будет исключено, и получится система вида:
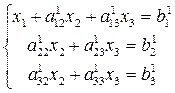 (3)
(3)
Теперь разделим второе уравнение системы (3) на 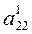 , умножим полученное уравнение на
, умножим полученное уравнение на 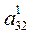 и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное
и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное 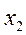 будет исключено и получится система треугольного вида:
будет исключено и получится система треугольного вида:
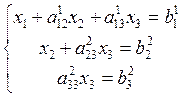 (4)
(4)
Из последнего уравнения системы (4) находим 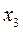 . Подставляя найденное
. Подставляя найденное 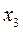 во второе уравнение, находим
во второе уравнение, находим 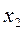 . Наконец, подставляя найденное значение
. Наконец, подставляя найденное значение 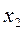 в первое уравнение, находим
в первое уравнение, находим 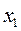 .
.
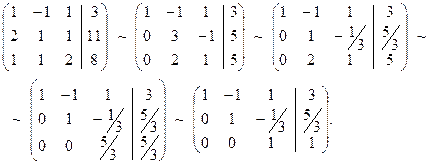
Последней матрице соответствует ступенчатая система уравнений:
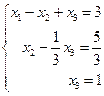 ,
,
равносильная исходной.
Из этой системы последовательно находим:
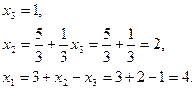
Таким образом: 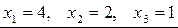 .
.
Выполним проверку, подставив найденные значения в исходную систему:
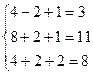 ,
,
Каждое уравнение системы обращается в верное равенство, следовательно, 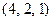 – единственное решение системы.
– единственное решение системы.
Задача 7. Вычислить пределы:
а) 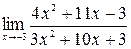 ; б)
; б) 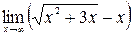 ;
;
в) 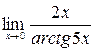 ; г)
; г) 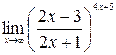 .
.
Решение.
а) Подстановка предельного значения аргумента 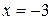 приводит к неопределенному выражению вида
приводит к неопределенному выражению вида 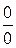 .
.
Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель 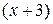 . Такое сокращение возможно, так как множитель
. Такое сокращение возможно, так как множитель 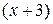 отличен от нуля при
отличен от нуля при 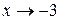 :
:
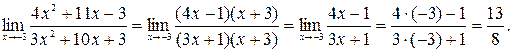
б) При 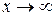 выражение
выражение 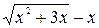 дает неопределенность вида
дает неопределенность вида 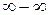 . Для ее устранения умножим и разделим это выражение на
. Для ее устранения умножим и разделим это выражение на 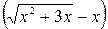 :
:
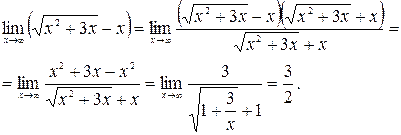
в) Обозначим 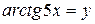 . Тогда
. Тогда 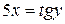 и
и 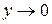 при
при 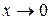 . Применяя свойства пределов и формулу первого замечательного предела
. Применяя свойства пределов и формулу первого замечательного предела 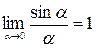 , имеем:
, имеем:
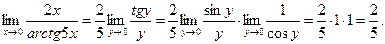
г) При 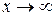 выражение
выражение 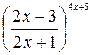 является неопределенностью вида
является неопределенностью вида 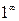 . Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при
. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при 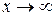 величины и применим формулу второго замечательного предела:
величины и применим формулу второго замечательного предела:
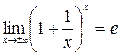 .
.
Тогда имеем:
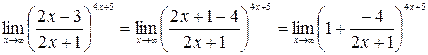 .
.
Пусть 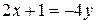 . Тогда
. Тогда 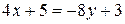 и
и 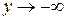 при
при 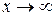 . Переходя к переменной у, получим:
. Переходя к переменной у, получим:
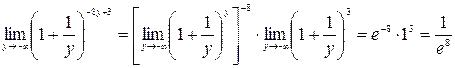 .
.