
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определители. 1.Определителем 2-го порядка называется число, вычисляемое по формуле
|
|
1. Определителем 2-го порядка называется число, вычисляемое по формуле
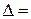
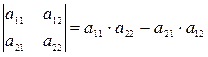 ,
,
где аij называется элементом определителя; первый индекс i указывает номер строки, а второй индекс j – номер столбца.
2. Определителем 3-го порядка называется число, вычисляемое по формуле (правило треугольников)

 а11 а12 а13
а11 а12 а13
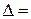 а21 а22 а23 = а11 а22 а33 + а21 а32 а13 + а12 а23 а31 – а31 а22 а13 – а21 а12 а33 –
а21 а22 а23 = а11 а22 а33 + а21 а32 а13 + а12 а23 а31 – а31 а22 а13 – а21 а12 а33 –
а31 а32 а33 -а32 а23 а11 .
3. Минором Мij элемента аij определителя 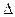 называется определитель, полученный из данного путем вычеркивания элементов i -ой строки и j -го столбца (на пересечении которых находится элемент аij).
называется определитель, полученный из данного путем вычеркивания элементов i -ой строки и j -го столбца (на пересечении которых находится элемент аij).
4. Алгебраическим дополнением Аij элемента аij данного определителя называется минор этого элемента, взятый со знаком (–1) i+j, т.е. Аij = (–1) i+j· Мij.
Ø ê = аi1 Аi1 + аi2 Аi2 + …+ аin Аin = 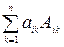
(разложение по элементам i -й строки, i = 1, 2, …, n);
Ø ê = а1j А1 j + а2 j А2 j + …+ аnj Аnj =
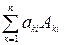 (разложение по элементам j -го столбца, j = 1, 2,.., n).
(разложение по элементам j -го столбца, j = 1, 2,.., n).
Свойства определителей
1. Замена всех строк соответствующими столбцами (транспонирование) не меняет значение определителя.
В дальнейшем строку или столбец будем называть рядом определителя.
2. Перестановка двух параллельных рядов меняет знак определителя.
3. Общий множитель всех элементов какого-нибудь ряда можно выносить за знак определителя.
4. Если все элементы какого-нибудь ряда равны нулю, то определитель равен нулю.
5. Определитель с двумя пропорциональными (равными) параллельными рядами равен нулю.
6. Сумма произведений элементов какого-нибудь ряда на алгебраические дополнения элементов параллельного ряда равна нулю.
7. Определитель не изменится, если к элементам какого-нибудь ряда прибавить элементы параллельного ряда, предварительно умноженные на одно и то же число.