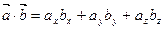Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Скалярное произведение векторов
|
|
|
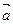 и
и 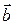 называется число (скаляр), равное произведению длин этих векторов на косинус угла j между ними.
называется число (скаляр), равное произведению длин этих векторов на косинус угла j между ними.
Свойства:
1) 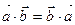 (переместительный закон)
(переместительный закон)
2) 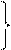
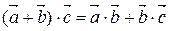 распределительный
распределительный
3) 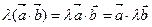 закон
закон
4) 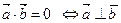
5) 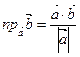 .
.
6) 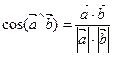
Выражение скалярного произведения через координаты
перемножаемых векторов
|
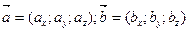 .
.
Тогда
Вопросы и задачи для зачета
1. Определители. Свойства определителей.
2. Минор, алгебраическое дополнение элементов определителя.
3. Матрицы. Действия над матрицами.
4. Обратная матрица и решение систем.
5. Ранг матрицы и его вычисление.
6. Системы линейных алгебраических уравнений. Правило Крамера.
7. Способ решения систем линейных уравнений методом Гаусса.
8. Теорема Кронекера-Капелли.
9. Вектор. Линейные операции над векторами.
10. Координаты вектора. Действия над векторами, заданными своими координатами. Деление отрезка в заданном отношении.
11. Скалярное произведение векторов и его свойства. Длина вектора. Угол между векторами.
12. Векторное произведение векторов и его геометрический смысл. Координатная форма векторного произведения.
13. Смешанное произведение векторов и его геометрический смысл. Координатная форма смешанного произведения векторов. Условие компланарности векторов.
14. Уравнение прямой на плоскости. Общее уравнение прямой. Нормальный вектор прямой.
15. Уравнение прямой, проходящей через две точки.
16. Уравнение прямой, проходящей через точку, параллельную заданному вектору. Направляющий вектор прямой.
17. Угол между двумя прямыми.
18. Условия параллельности и перпендикулярности прямых.
19. Расстояние от точки до прямой.
20. Уравнение плоскости, проходящей через точку перпендикулярно вектору.
21. Общее уравнение плоскости. Нормальный вектор плоскости.
22. Уравнение плоскости, проходящей через три точки.
23. Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.
24. Расстояние от точки до плоскости.
25. Каноническое уравнение прямой в пространстве. Направляющий вектор прямой.
26. Уравнение прямой, как линии пересечения двух плоскостей.
27. Условия параллельности и перпендикулярности прямой и плоскости.
28. Угол между прямой и плоскостью.
29. Кривые второго порядка. Окружность. Уравнение окружности.
30. Эллипс. Каноническое уравнение эллипса. Эксцентриситет эллипса.
31. Гипербола. Каноническое уравнение гиперболы.
32. Парабола. Каноническое уравнение параболы.
33. Функция. Область определения, область изменения функции. Способы задания функции.
34. Графики степенных функций.
35. Графики показательной и логарифмической функций.
36. Четность, нечетность функции. Корни функции.
37. Периодические функции. Графики основных тригонометрических функций.
38. Обратные и сложные функции.
39. Предел функции в точке. Теоремы о пределах.
40. Непрерывность функции в точке и на отрезке.
41. Точки разрыва функции. Классификация точек разрыва.
42. Свойства функций, непрерывных на отрезке.
Задачи
1. Для прямой 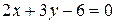 найти угловой коэффициент и построить ее график.
найти угловой коэффициент и построить ее график.
2. Найти уравнение прямой, проходящей через точку 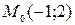
а) перпендикулярно, б) параллельно прямой 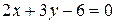 .
.
3. Найти уравнение прямой, проходящей через две точки 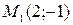 и
и 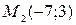 .
.
4. Построить эллипс 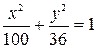 и найти координаты фокусов.
и найти координаты фокусов.
5. Для гиперболы 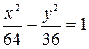 найти эксцентриситет
найти эксцентриситет  .
.
6. Построить параболу 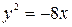 и найти координаты ее фокуса.
и найти координаты ее фокуса.
7. Построить параболу 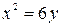 и найти координаты ее фокуса.
и найти координаты ее фокуса.
8. Найти длину вектора 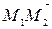 , если
, если 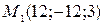 и
и 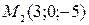 .
.
9. Найти угол между векторами 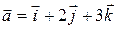 и
и 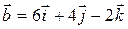 .
.
10. При каком значении т векторы 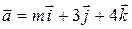 и
и 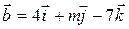 перпендикулярны?
перпендикулярны?
11. Вычислить определитель 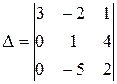 .
.
12. Найти 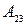 для элемента
для элемента 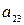 матрицы
матрицы 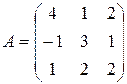 .
.
13. Решить систему уравнений методом Гаусса
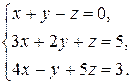
14. Найти: а) 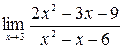 ,
,
б) 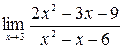 ,
,
в) 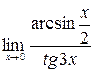 .
.
Список литературы
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. -М.: Наука, 1985.
2. Беклемишева Л.А., Петрович А.Ю., Чубаров И. А. Сборник задач по аналитической геометрии и линейной алгебре. -М.: Наука, 1987.
3. Берман Г.Н. Сборник задач по курсу математического анализа. М.: Наука, 1972.
4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. -М.: Наука, 1980.
5. Данко П.Е., Попов А. Г., Кожевникова Т.Е. Высшая математика в упражнениях и задачах. В 2 ч. М., 1980.
6. Ильин В.А., Позняк Э.Г. Основы математического анализа. В 2 ч.-М.: Наука, 1982.
7. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. -М.: Наука, 1982.
8. Марон И.А. Дифференциальное и интегральное исчисление в примерах и задачах. -М.: Наука, 1965.
9. Минорский В.Д. Сборник задач по высшей математике. -М.: Наука, 1987.
10. Мышкис А.Д. Лекции по высшей математике. -М.: Наука, 1973.
11. Пискунов Н.С. Дифференциальное и интегральное исчисление. В 2т. -М.: Наука, 1968.
12. Проскуряков И.В. Сборник задач по линейной алгебре. -М.: Наука, 1984.
13. Сборник задач по математике. В 4ч. (Под редакцией Ефимова А.В., Демидовича Б.П.) -М.: Наука, 1981. Ч. 1-2.
14. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. -М.: Наука, 1966.
[1] Рекомендуем сдавать работу на проверку несколько раньше, т.к. в случае отрицательной рецензии на переработку контрольной работы потребуется дополнительное время, приходящее на зачетную сессию. Напоминаем, что студент, не получивший зачет по данной работе, к итоговому зачету допущен не будет.