Частотные критерии устойчивости

3.3.1 Критерий Михайлова

Пусть передаточная функция (ПФ) W(s) системы n-го порядка представляет собой отношение полиномов от s:

.

Произведём подстановку s = jw в знаменатель ПФ. При изменении частоты w вектор A(jw), изменяясь по величине и направлению, будет описывать своим концом в комплексной плоскости некоторую кривую, называемую кривой (годографом) Михайлова.

Критерий Михайлова формулируется следующим образом: для того, чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы вектор А(jw) кривой Михайлова при изменении частоты w от 0 до +¥ повернулся, нигде не обращаясь в нуль, вокруг начала координат против часовой стрелки на угол π n/2, где n-порядок характеристического уравнения А(l) =0.

3.3.2 Критерий Найквиста

Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по виду амплитудно-фазовой характеристики разомкнутой системы

W_р(jw) = B(jw)/A(jw).

Если система в разомкнутом состоянии устойчива, то и замкнутая система будет устойчивой, если амплитудно-фазовая характеристика разомкнутой системы не охватывает точку (− 1, j0).

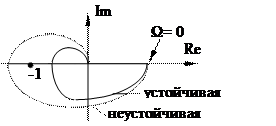Рисунок 3 - Графическая интерпретация критерия Найквиста

Достоинством критерия Найквиста является применимость его тогда, когда АФЧХ разомкнутой АС получена экспериментальным путем.

Для расчётных целей существуют обобщения критерия Найквиста на случай, когда разомкнутая АС является неустойчивой (например, содержит интегрирующие звенья или уравнение A(s) = 0 имеет положительные корни). Дело в том, что экспериментально у таких АС ЧХ снять невозможно.

3.3.3 Запас устойчивости..

Запас устойчивости по фазе определяют как величину угла 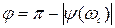для частоты ω _с, при которой 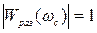, по амплитуде – как величину отрезка абсцисс h, заключённого между критической точкой (-1; j0) и АФЧХ.