
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка устойчивости с помощью частотных критериев
|
|
4.3.1 Оценка устойчивости с использованием критерия Михайлова
В качестве примера оценим с помощью критерия Михайлова устойчивость системы третьего порядка, характеристическое уравнение которой имеет вид:
s3 + s2 + s + 4 = 0.
Для построения годографа Михайлова сначала задаются набором частот CHAST, а затем, пользуясь функцией polyval, вычисляют вектор комплексных значений характеристического полинома. В качестве аргумента этой функции берется сформированный вектор частот CHAST, элементы которого умножены на мнимую единицу j. По оси абсцисс откладывается вещественная часть (real), по оси ординат – мнимая часть (imag) годографа Михайлова. В целом последовательность действий может быть такой:
CHAST=0: 0.1: 2.2;
POL=[1 1 1 4];
xar=polyval(POL, j*CHAST);
x=real(xar);
y=imag(xar);
plot(x, y); grid; title('Годограф Михайлова'); xlabel('реальная'); ylabel('мнимая');
В результате на экране монитора воспроизводится годограф Михайлова:
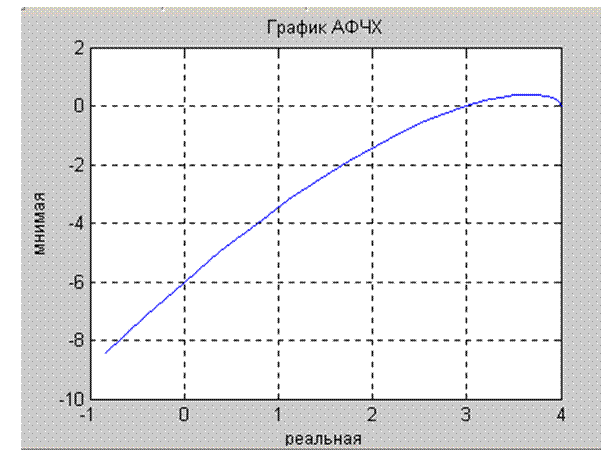
Итак, система третьего порядка не является устойчивой, так как годограф Михайлова не проходил при изменении частоты w от 0 до +¥ через второй квадрант.
4.3.2 Оценка устойчивости с использованием критерия Найквиста
Частотные критерии целесообразно изучать, исследуя устойчивость систем с помощью функций nyquist, которые предназначены для расчета и построения в комплексной области частотного годографа Найквиста, то есть графика амплитудно-фазовой характеристики системы:
Имеются две формы задания функции nyquist:
nyquist(m)
[re, im]=nyquist(m, w),
где m – идентификатор исследуемой системы, аргумент w задает набор частот(w=[w1, w2, …, wn]), re и im –соответственно векторы значений вещественной и мнимой частей комплексного коэффициента передачи для заданного набора частот. Для оценки устойчивости системы вполне достаточно использовать лишь первую форму функции nyquist.
Примеры:
m=tf([8], [0.1 1])
Transfer function:
---------
0.1 s + 1
nyquist(m)
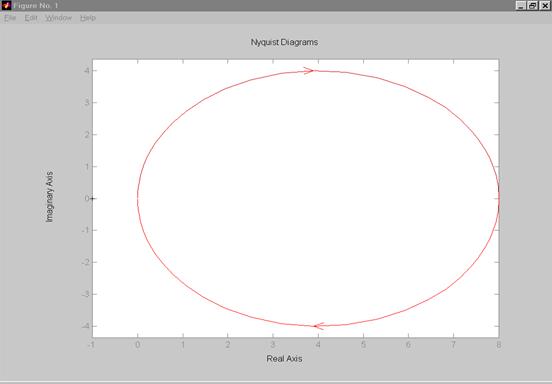
На данном графике по оси X откладывается вещественная часть передаточной функции, по оси Y– мнимая часть. Каждой частоте частотного диапазона соответствует единственная точка графика АФЧХ, всю информацию для которой можно воспроизвести на экране монитора, поместив в эту точку курсор и нажав левую кнопку мыши.
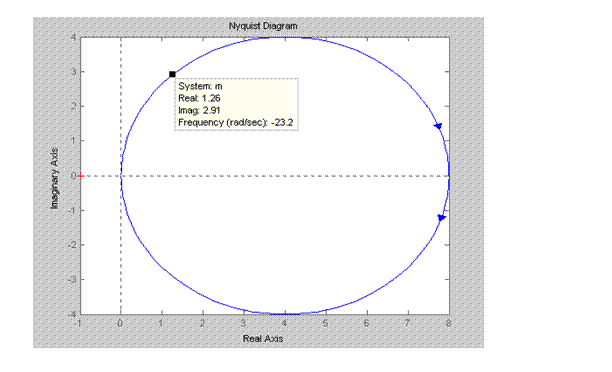
При этом воспроизводятся: идентификатор исследуемой системы, значения вещественной и мнимой частей комплексного коэффициента передачи для частоты, соответствующей данной точке графика, и величина этой частоты (в рад/с). Красным крестиком отмечена точка (− 1, j0).
Система с идентификатором m в разомкнутом состоянии устойчива (имеет единственный полюс в отрицательной полуплоскости); в замкнутом состоянии эта система также будет устойчивой, так как ее амплитудно-фазовая характеристика в разомкнутом состоянии не охватывает точку (− 1, j0).