Показатели вариации

Для более полной характеристики изучаемого признака рассчитываются показатели вариации. Вариация – различие значений признака у отдельных единиц изучаемой совокупности в один и тот же период или момент времени. Статистический анализ вариации предполагает выполнение следующих основных этапов:

1. построение вариационного ряда;

2. графическое изображение вариационного ряда;

3. расчет показателей центра распределения и структурных характеристик вариационного ряда;

4. расчет показателей размера и интенсивности вариации;

5. Оценка вариационного ряда на ассиметрию и эксцесс.

Показатели вариации – это показатели колеблемости признака относительно своего центра 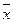(или 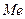). Различают показатели размера и интенсивности вариации.

К показателям размера вариации относят:

• размах вариации

R = x_max - x_min, (18) устанавливающий предельное значение амплитуды колебаний признака;

• межквартильный размах

R_M (Q₃ – Q₁), (19)

определяющиймаксимальную амплитуду колебаний в центральной зоне ряда (ограниченной квартилями Q₁ и Q₃);

• среднее линейное отклонение, вычисляемое как среднее арифметическое из абсолютных отклонений ;
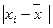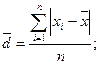• (20)

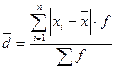(21)

• дисперсия 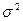, рассчитываемая как среднее арифметическое из квадратов отклонений :

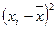В зависимости от исходных данных её исчисляют по формуле средней квадратической простой:

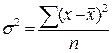, (22)

или взвешенной:

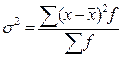(23)

• Среднее квадратическое (стандартное) отклонение 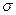, вычисляемое как корень квадратной из дисперсии :

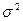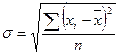(простое) (24)

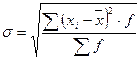(взвешенное) (25)

Интенсивность вариации признака измеряется относительными показателями:

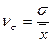• - коэффициент вариации; (26)
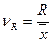• - коэффициент осцилляции (27)
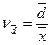• (28)
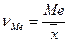• (29)

Показател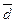и , и 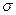являются величинами именованными и выражаются в тех же единицах, что и изучаемый признак. Дисперсия 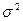считается безразмерной величиной. Относительные показатели интенсивности вариации, как правило, измеряются в процентах.

Величина 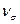оценивает интенсивность колебаний вариантов относительно их средней величины. Принята следующая оценочная шкала колеблемости

признака:

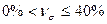- колеблемость незначительная

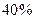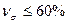< - колеблемость средняя (умеренная)

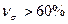- колеблемость значительная.

Для нормальных и близких к нормальному распределений показатель 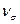служит индикатором однородности совокупности. Принято считать, что при выполнении неравенства (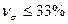) совокупность является качественно однородной по данному признаку, а средняя - типичной величиной.

Относительные показатели вариаци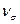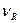и , и 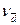используются для сравнения колеблемости признаков:

• когда сравнивается вариация разных признаков в одной и той же совокупности;
• когда сравнивается вариация одного и того же признака в различных совокупностях, имеющих разные средние .

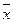Среди признаков, изучаемых статистикой, есть и такие, которым свойственны лишь два взаимоисключающих значения, Такие признаки называются альтернативными. Им придается соответственно два количественных значения: 1 и 0. Частостью варианта 1 (она обозначается 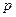) является доля единиц, обладающих данным признаком, в общей численности совокупности. Разность 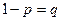является частостью варианта 0.

Дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, и доли единиц, не обладающих этим признаком.

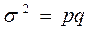(30)

Среднее квадратическое отклонение:

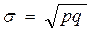(31)

Если значения 1 и 0 встречаются одинаково, т.е. 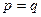, то дисперсия достигает своего максимума .

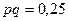Дисперсия альтернативного признака используется в выборочных обследованиях, например, качества продукции.