Моменты распределения. Показатели особенностей формы распределения

Для подробного описания особенностей распределения используются дополнительные характеристики, в частности, моменты распределения. Момент распределения – средняя арифметическая различных степеней отклонений индивидуальных значений признака от определенной постоянной величины. Система моментов распределения была разработана русским математиком П.Л. Чебышевым.

Наиболее общее математическое выражение момента распределения записывается в виде формулы:

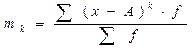, (37)

где 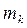- момент k-ro порядка

x - варианты ряда

f - частоты ряда

А - величина, от которой определяются отклонения

k - степень отклонения (порядок момента)

В зависимости от того, что принимается за величину А, различают три вида моментов:

1. при А=0 получают систему начальных моментов. Начальный момент k-го порядка выражается формулой:

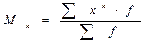(38)

Начальный момент первого порядка 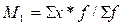, т.е. известная уже средняя арифметическая взвешенная. Начальный момент второго порядка 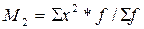, т.е. средняя из квадратов вариантов, которая также упоминалась ранее.

2. При 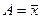получаем систему центральных моментов. Центральный момент k-го порядка выражается формулой:

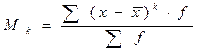(39)

Центральные моменты - это средние из различных степеней отклонений от средней арифметической:

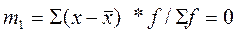
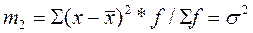
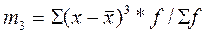и т.д.

Центральный момент первого порядка (в соответствии с нулевым свойством средней арифметической) всегда равен нулю. Центральный момент второго порядка представляет собой дисперсию. Центральный момент третьего порядка равен нулю в симметричном распределении и используется для определения показателя а симметрии. Центральный момент четвёртого порядка применяется при вычислении показателя эксцесса.

3. При А, не равной средней арифметической и отличной от нуля (обычно близкий к его середине), получаем условные моменты:

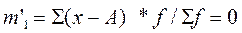(40)

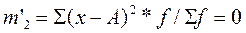(41)

Начальные моменты второго, третьего и четвёртого порядков так же, как и условные моменты, самостоятельного значения не имеют, а используются для упрощения вычислений центральных моментов. Например, используя начальные моменты первого и второго порядка, можно получить дисперсию:

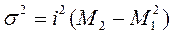(42)

В практике статистического исследования приходится встречаться с самыми различными распределениями. Однородные совокупности характеризуются, как правило, одновершинными распределениями. Многовершинность свидетельствует о неоднородности изучаемой совокупности. Появление двух и более вершин говорит о необходимости перегруппировки данных с целью выделения более однородных групп.

Форма распределения признака в вариационных рядах распределения отражает закономерность изменения частот с ростом значений варьируемого признака. Обобщающие характеристики формы распределения получают, используя кривые распределения. Они бывают эмпирическими и теоретическими.

Эмпирическая кривая распределения – фактическая кривая распределения, построенная по данным наблюдения, отражает как общие, так и случайные условия, определяющие распределение признака.

Теоретическая кривая распределения выражает функциональную связь между варьирующим признаком и частотами. Она отражает основную закономерность распределения признака при полном погашении случайных причин.

Симметричным я вляется распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричных распределений имеет место равенство средней арифметической, моды и медианы.

В случае асимметричного распределения вершина кривой находится не в середине, а сдвинута либо влево, либо вправо.

Если вершина сдвинута влево, то правая часть кривой оказывается длиннее левой, т.е. имеет место правосторонняя асимметрия, характеризующаяся неравенством

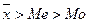, (43)

что означает преимущественное появление в распределении более высоких значений признака.

Если же вершина кривой сдвинута вправо и левая часть оказывается длиннее правой, то асимметрия левосторонняя, для которой справедливо неравенство

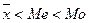, (44)

означающее, что в распределении чаще встречаются более низкие значения признака.

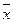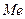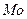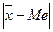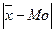Чем больше величина расхождения между , , , тем более асимметричен ряд. Разности и являются простейшими показателями асимметрии в рядах распределения.

В нормальном и близких к нему распределениях основная масса единиц (почти 70%) располагается в центральной зоне ряда, в диапозоне 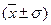. Для оценки асимметричности распределения в этом центральном диапозоне служит коэффициент К. Пирсона:

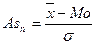(45)

При правосторонней асимметрии 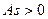, при левосторонней 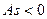. Если 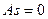, вариационный ряд симметричен.

Наиболее точным и распространенным является коэффициент асимметрии 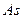, основанный на определении центрального момента третьего порядка (в симметричном распределении его величина равна нулю):

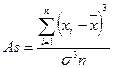, (46)

где 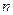- число единиц совокупности.

Чем больше 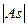, тем более асимметрично распределение. Установлена следующая оценочная шкала асимметричности:

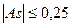- асимметрия незначительная;

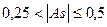- асимметрия заметная (умеренная);

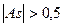- асимметрия существенная.

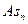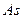Поскольку коэффициенты и являются относительными безразмерными величинами, они часто применяются для сравнительного анализа асимметричности различных рядов распределения.

Для симметричных или близких к ним распределений рассчитывается коэффициент эксцесса .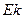

Показатель эксцесса характеризует крутизну кривой распределения –ее заостренность или пологость по сравнению с нормальной кривой

Наиболее точным является показатель, основанный на использовании центрального момента четвёртого порядка:

(47)