
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Необходимая численность выборки
|
|
Рассмотренные формулы позволяют рассчитать предварительно, какую необходимо взять численность выборки, чтобы ошибка выборки не превышала определенных заданных размеров.
В практике при проектировании выборочного наблюдения всегда определяется его численность.
Если средняя ошибка для выборочной средней определялась по формуле:
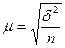 , то
, то 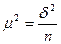 à
à 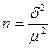
то есть необходимая численность выборки для выборочной средней равна среднему квадрату отклонений, деленному на квадрат заданной точности. Под точностью понимается допустимая ошибка выборки.
Если в формулу ввести коэффициент t, то она примет вид:
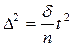 , откуда
, откуда 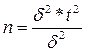 .
.
При выборочном измерении доли признака:
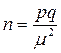 ,
,
Необходимая численность выборки равна доле, умноженной на дополнение ее до единицы и деленной на квадрат заданной точности.
Если в формулу ввести коэффициент t (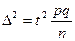 ), тогда
), тогда
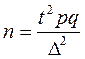
Для бесповторного отбора необходимая численность выборки:
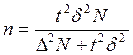 - для выборочной средней,
- для выборочной средней,
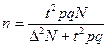 - для выборочной доли.
- для выборочной доли.
Поскольку 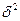 и р заранее неизвестны, принимают
и р заранее неизвестны, принимают 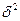 из предыдущих обследований или пробных наблюдений, а р берут равным 0, 5; тогда при выборочном измерении доли признака необходимая численность выборки:
из предыдущих обследований или пробных наблюдений, а р берут равным 0, 5; тогда при выборочном измерении доли признака необходимая численность выборки:
Для повторного отбора:
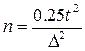 или
или 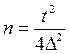
Для бесповторного отбора:
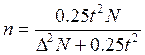 .
.
Пример 1. Для анализа объемов продаж предприятий одной из отраслей региона в отчетном периоде была проведена 10% механическая выборка, в результате которой было отобрано 20 фирм. Требуется с вероятностью 0, 954 определить средний объем продаж предприятий генеральной совокупности, если известно, что средний объем продаж фирм выборочной совокупности составил 3, 105 млн. руб., а среднее квадратическое отклонение равно 0, 34 млн. руб.