
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Выборочная средняя и выборочная дисперсия
|
|
Пусть проведена выборка объема n.
Выборочной средней 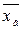 называется среднее арифметическое значений выборки.
называется среднее арифметическое значений выборки.
Если все значения выборки различны, то
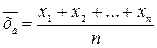 .
.
Если же варианты x1, x2, …xk имеют соответственно частоты n1, n2, …, nk, то
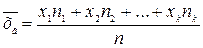
или
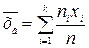 ,
,
где n1 + n2+ …+ n k = n.
В некоторых случаях выборочные значения случайной величины целесообразно разбивать на отдельные группы. В каждой группе можно найти ее среднюю.
Групповой средней 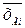 называют среднее для всей выборки.
называют среднее для всей выборки.
По этим групповым средним можно найти среднее для всей выборки.
Общей средней 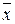 называют среднее арифметическое значение групповых средних.
называют среднее арифметическое значение групповых средних.
Пример. Найти общую среднюю на основе выборки:
| Группа | ||||
| Значение варианты | ||||
| Частота | ||||
| Объем |
Решение. Находим групповые средние:
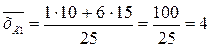 ,
,
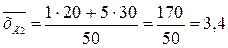 .
.
Общая средняя 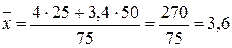 .
.
Ответ. 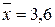 .
.
Для характеристики рассеяния выборочных значений относительно выборочного среднего вводится понятие выборочной дисперсии.
Выборочной дисперсией 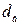 называется среднее арифметическое квадратов отклонений наблюдаемых значений от выборочного среднего.
называется среднее арифметическое квадратов отклонений наблюдаемых значений от выборочного среднего.
Если все значения выборки различны, то
 .
.
Если значения выборки имеют соответствующие частоты, то
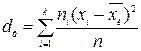 .
.
Выборочным средним квадратичным отклонением называется арифметический квадратный корень из выборочной дисперсии:
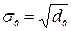 .
.