
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод наибольшего правдоподобия для точечной оценки параметров распределения
|
|
Пусть Х – дискретная случайная величина, которая при выборке объемом n получила значения x1, x2, …xn. Допустим, что известен вид закона распределения вероятностей, но неизвестен параметр 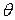 .
.
Обозначим через 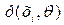 вероятность того, что величина Х принимает значения xi (i=1, …, n).
вероятность того, что величина Х принимает значения xi (i=1, …, n).
Функцией правдоподобия дискретной случайной величины называю функцию
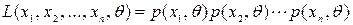 .
.
Точечной оценкой параметра 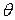 считается такое значение
считается такое значение 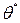 , при котором функция L принимает наибольшее значение. Эту оценку называют оценкой наибольшего правдоподобия.
, при котором функция L принимает наибольшее значение. Эту оценку называют оценкой наибольшего правдоподобия.
Так как функции L и ln L обычно принимают наибольшее значение при одном и том же 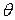 , то оценку
, то оценку 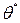 определяют на основе максимизации функции ln L. Для этого функцию исследуют на максимум с помощью необходимого (а иногда и достаточного) условия экстремума.
определяют на основе максимизации функции ln L. Для этого функцию исследуют на максимум с помощью необходимого (а иногда и достаточного) условия экстремума.
Этот метод эффективен в случае малых выборок, но часто требует довольно сложных вычислений.