Анализ смещенности выборочной средней и выборочной дисперсии

Выборочная средняя 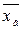является несмещенной оценкой, а выборочная дисперсия 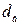- смещенной оценкой.

Пусть дана выборка x₁, x₂, …x_n. Будем рассматривать выборочные значения как реализации случайных величин Х₁, Х₂, …Х_n, одинаково распределенных по закону распределения генеральной совокупности, т.е. случайной величины Х. Это означает, что они имеют одно и тоже математическое ожидание M_x и дисперсию .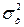

Математическое ожидание выборочной дисперсии не равно оцениваемой дисперсии генеральной совокупности 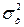. Чтобы «исправить» выборочную дисперсию, ее нужно умножить на дробь .

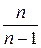В результате получим «исправленную» выборочную дисперсию

.

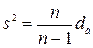Соответственно, «исправленным» выборочным квадратичным отклонением называется арифметический квадратный корень из «исправленной» выборочной дисперсии.

Теорема. Выборочная дисперсия равна среднему арифметическому квадратов значений выборки минус квадрат выборочной средней:

.
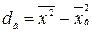