
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод моментов для точечной оценки параметров распределения
|
|
Пусть известен вид функции плотности распределения вероятностей случайной величины, зависящей от одного неизвестного параметра 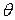 .
.
Например, 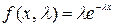 - показательное распределение (
- показательное распределение (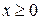 ). Требуется найти точечную оценку параметра
). Требуется найти точечную оценку параметра 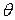 . В случае показательного распределения
. В случае показательного распределения 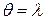 .
.
Для получения оценки одного параметра можно использовать одно уравнение с одним неизвестным. В методе моментов в качестве такого уравнения предлагается равенство
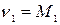 ,
,
где 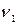 - начальный теоретический момент первого порядка;
- начальный теоретический момент первого порядка;
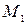 - начальный эмпирический момент первого порядка.
- начальный эмпирический момент первого порядка.
Теоретический момент первого порядка представляет собой математическое ожидание, а эмпирический момент первого порядка – это выборочная средняя. Таким образом,
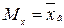 .
.
Для экспоненциального распределения 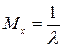 . Тогда для оценки
. Тогда для оценки 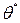 :
:
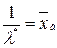 ,
, 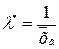 .
.
Если плотность распределения вероятностей зависит от двух параметров, 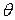 нужно искать как двумерный вектор. Для оценки этих параметров требуется составлять не одно, а два уравнения. Такими уравнениями могут быть равенства:
нужно искать как двумерный вектор. Для оценки этих параметров требуется составлять не одно, а два уравнения. Такими уравнениями могут быть равенства:
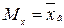 ,
, 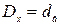 или, что более точно,
или, что более точно, 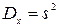 .
.