Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Простая линейная регрессия
|
|
Простаялинейная регрессия используется для исследования зависимости двух переменных. Уравнение простой линейной регрессии можно записать в виде
yi = a0 + a1xi + ei(2)
где e1, …en- независимые одинаково распределенные случайные величины, определяющие действие различных неучтенных факторов на изменение результирующего показателя Y.
Для определения оценок параметров в уравнении (2) широко используется метод наименьших квадратов (МНК), суть которого заключается в следующем.
Определим величину ei следующим образом:
ei = yi – (a0 + a1xi).
Величина ei называется отклонением (остатком) наблюдаемого значения результирующей переменной yi в i – ом наблюдении от расчетного. Отклонение ei является оценкой случайной компоненты ei. Построим оценку параметров (a0, a1) так, чтобы сумма их квадратов отклонений была минимальной:
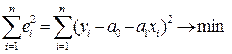(3)
Сумму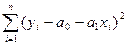 
минимимизируем по (a0, a1), приравнивая нулю соответствующие производные.В результате получим систему уравнений линейных относительно a0 и a1. Ее решение 
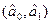легко находится:
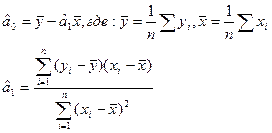(4) и (5)
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции ryx. Для линейной регрессии (-1≤ ryx≤ 1)
ryx = a1sx/sy
sx =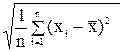 
, sy = 
,
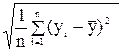здесь sx и sy - стандартные (среднеквадратические) отклонения по x и y.