Множественная регрессия

Обобщением линейной регрессионной модели с двумя переменными является многомерная регрессионная модель (или модель множественной регрессии). Уравнение линейной регрессии 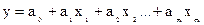. В экономике широко используется степенная функция вида: 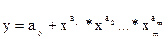. Эта функция используется для изучения спроса и потребления, для построения производственной функции, где y – выпуск, а x – факторы производства и др.

Коэффициенты линейной модели уравнения регрессии называются коэффициентами чистой регрессии. В случае полинома 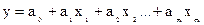коэффициенты характеризуют среднее изменение результата, при изменении соответствующего фактора на одну единицу и при неизменной величине остальных факторов.

В степенной функции коэффициенты чистой регрессии показывают, на сколько процентов изменится результат, при изменении соответствующего фактора на один процент и при фиксированном значении остальных факторов. Они играют роль коэффициентов эластичности.

Решение уравнения регрессии находится с помощью метода наименьших квадратов. Анализ полученного решения заключается в проверке полученного уравнения регрессии путем расчета коэффициента множественной детерминации:

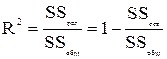
и F – статистики:

.

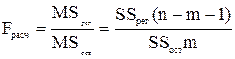Если известен коэффициент детерминации R², то F – статистка может быть рассчитана следующим образом:

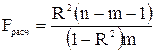
Рассчитанное значение сравнивается с табличным F_{df1, df2, α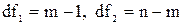} (), где m – число независимых переменных, n – число наблюдений. Либо для расчетного значения F – статистики определяется P – уровень, который сравнивается с уровнем значимости α, так как это было описано в предыдущем разделе.

Недостатком коэффициента детерминации является то, что он увеличивается при добавлении новых переменных, хотя это и не обязательно означает улучшения качества регрессионной модели. Поэтому лучше пользоваться скорректированным коэффициентом детерминации, который определяется по формуле:

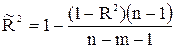
Уравнение регрессии может быть преобразовано к стандартизованному масштабу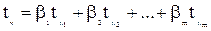

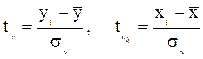, где j – номер переменной.

Значения коэффициентов b_j можно определить из уравнения:

,

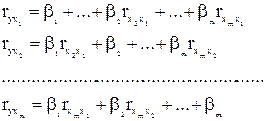где 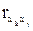- коэффициенты взаимной корреляции между x_k и x_j.

Основное достоинство стандартизованного уравнения регрессии в том, что стандартизованные коэффициенты b_j сравнимы между собой и позволяют ранжировать факторы по степени их воздействия на результат.

Коэффициенты чистой регрессии b_j связаны со стандартизованными коэффициентами b_j соотношением

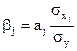
Проверка значимости коэффициентов регрессии аналогична проверке коэффициентов парной регрессии и сводится к вычислению значения

,

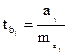где 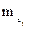- средняя квадратическая ошибка коэффициента регрессии b_j