Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Пример решения типового расчета по теме
|
|
Пример решения типового расчета по теме
«Дифференциальные уравнения и системы»
Дифференциальные уравнения первого порядка.
1. Найти частное решение, удовлетворяющее заданному начальному условию (решить задачу Коши):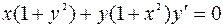 
; 
.
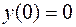Решение.
Найдем сначала общее решение данного ДУ.
Заменим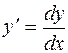 
и запишем уравнение в симметричной форме:
) 
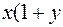
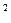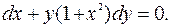
(1)
Это уравнение является дифференциальным уравнением с разделяющимися 
переменными (Р.П.), т.к. коэффициентами при дифференциалах являются функции только одной переменной.
Разделим переменные в (1), умножив обе части ДУ на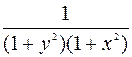 
, тогда уравнение примет вид: 
.
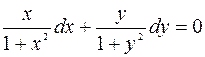Интегрируя, получим:
.
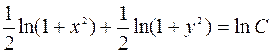(Произвольную постоянную удобно обозначить через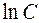 
).
Используя свойства логарифмов, запишем общее решение ДУ в виде:
. 
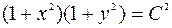Найдём частное решение, удовлетворяющее начальному условию
: 
.
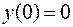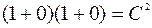
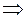
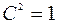Итак, 
– частное решение.
Ответ: .
2. Найти общее решение ДУ: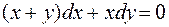 
.