Решение. Данное ДУ содержит в правой части две функции специального вида

Данное ДУ содержит в правой части две функции специального вида. Будем искать его решение в виде: , где 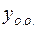– общее решение однородного уравнения, а 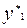и 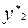– некоторые частные решения неоднородного уравнения, соответствующие каждой из функций.

Характеристическое уравнение имеет корни .

Тогда общее решение соответствующего однородного уравнения имеет вид:

.

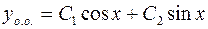Будем интегрировать уравнение (11) отдельно для каждого слагаемого, стоящего в правой части уравнения.

1) ;

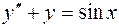Частное решение ищем в виде: .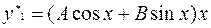

Методом неопределенных коэффициентов находим:

.

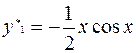2) ;

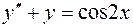Частное решение ищем в виде: .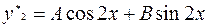

Методом неопределенных коэффициентов находим:

.

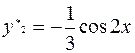Окончательно имеем: – общее решение неоднородного уравнения.

Ответ: .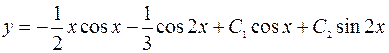

12. Найти общее решение ДУ: .