Решение. Это – линейное уравнение относительно неизвестной функции и её производной

Это – линейное уравнение относительно неизвестной функции и её производной. Используем метод Бернулли.

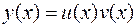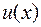Будем искать общее решение в виде , где и 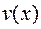– неизвестные функции аргумента .

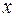Подставим решение 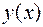в уравнение:

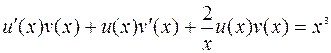или .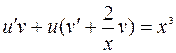

Выберем функцию 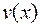так, чтобы 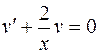, тогда для функции 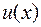получим уравнение: .

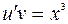Решаем систему: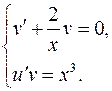

Замечание: в первом уравнении находим любое частное решение 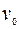, а во втором – общее решение.

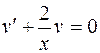
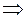
1) 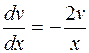(Р.П.) .

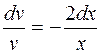
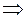
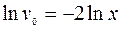
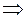
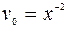(Произвольную постоянную берём равной нулю!).

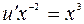
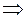
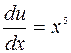
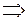
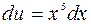
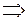
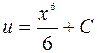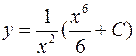2) . Следовательно, – общее решение ДУ.

Ответ: .

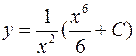4. Найти общее решение ДУ: .

Решение.

Это уравнение Бернулли. Оно приводится к линейному уравнению подстановкой: .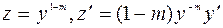

У нас ; .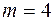

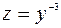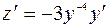Подставляем в данное уравнение:

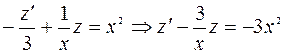– это линейное уравнение относительно 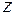и .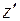

Решаем полученное уравнение методом Бернулли.

Делаем подстановку :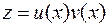

;

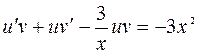
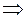
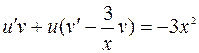
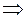
1) ;

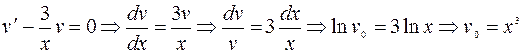2) ;

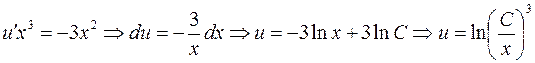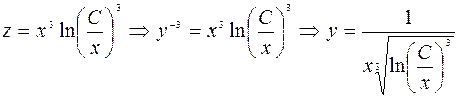–общее решение.

Ответ: .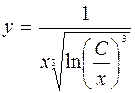

5. Найти общее решение ДУ: 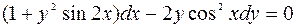.