Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Убедимся, что данное ДУ является дифференциальным уравнением в полных дифференциалах.
|
|
Убедимся, что данное ДУ является дифференциальным уравнением в полных дифференциалах.
Имеем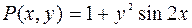 
; 
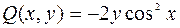, тогда 
; 
.
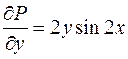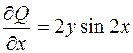Видим, что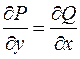 
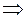это ДУ в полных дифференциалах, т.е. левая часть уравнения является полным дифференциалом некоторой функции 
.
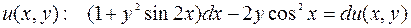Общее решения будет иметь вид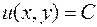 
.
Найдем функцию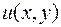 
с помощью формулы:
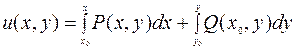, где 
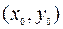– любая точка, для которой интегралы имеют смысл.
Возьмём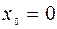 
и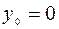 
. Тогда
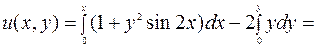
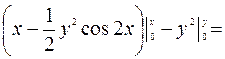
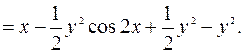
Следовательно,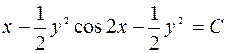 
– общий интеграл ДУ.
Ответ: .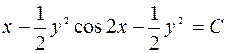
Дифференциальные уравнения высших порядков.
ДУ, допускающие понижение порядка.
6. Найти общее решение ДУ: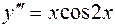 
.
Решение.
Данное уравнение является дифференциальным уравнением третьего порядка, допускающее понижение порядка непосредственным интегрированием.
=
= 
.
= 
= 
= 
= 
.
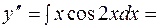
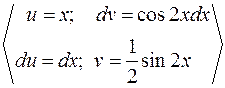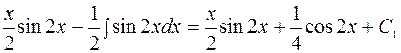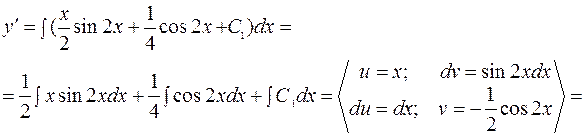
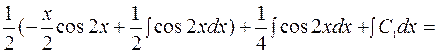
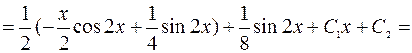
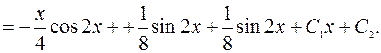
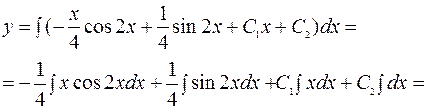
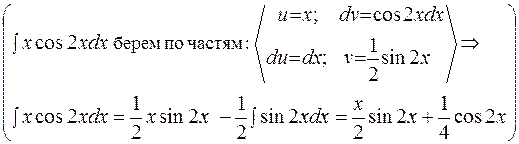
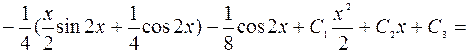
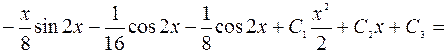
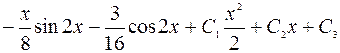Ответ: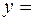 
.
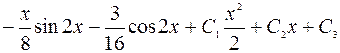7. Найти общее решение ДУ: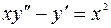 
.
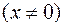