Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
в) Операторный метод.
|
|
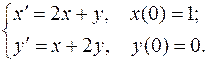
Введем изображения искомых функций и их производных:
, 
,
,
.
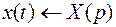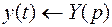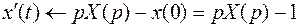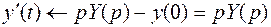Тогда система примет вид:
.
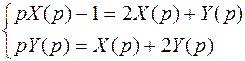
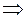
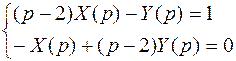Решим системы методом Крамера:
;
; 
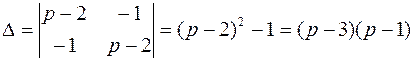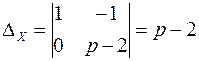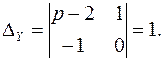
Откуда:
; 
.
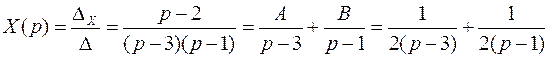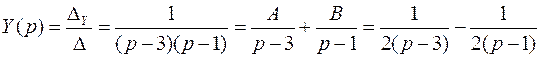По таблицам преобразования Лапласа находим частное решение системы дифференциальных уравнений:
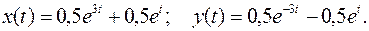
Ответ: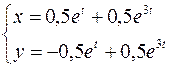 
14. Найти общее решение системы ДУ: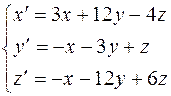 
.
Решение:
Будем решать эту систему алгебраическим методом.
Ищем решения в виде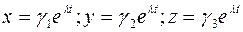 
.
Подставим в систему, получим:
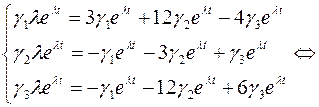
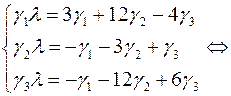
Составим характеристическое уравнение:
.
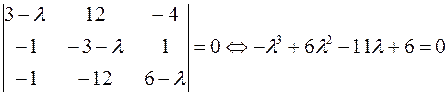Решая уравнение, находим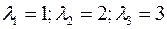 
–характеристические числа. Подставим их в систему 
.
.
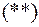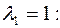
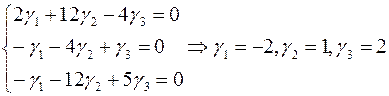Тогда,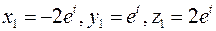 
– частное решение, соответствующее корню 
.
.
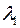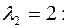
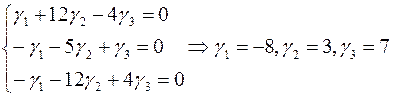Тогда,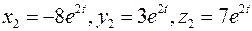 
частное решение, соответствующее корню 
.
.
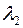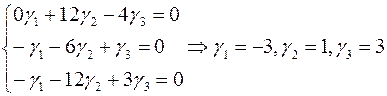Тогда,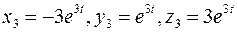 
частное решение, соответствующее корню 
.
Общее решение системы будет иметь вид:
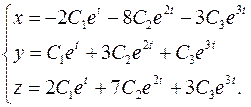
Ответ: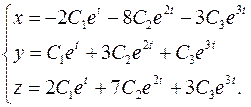
15. Составить уравнение кривой, проходящей через точку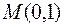 
и обладающей тем свойством, что в каждой её точке угловой коэффициент касательной равен удвоенной абсциссе точки касания.
Решение:
Обозначим за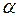 
угол, образованный касательной к искомой кривой 
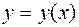в произвольной точке 
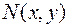этой кривой (Рис. 1). Тогда 
.
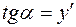По условию задачи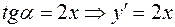 
– дифференциальное уравнение.
Общее решение этого дифференциального уравнения: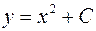 
.
Найдём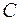 
, используя условие задачи:
.
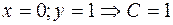Тогда уравнение искомой кривой будет иметь вид: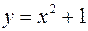 
.
Это уравнение параболы.
 |
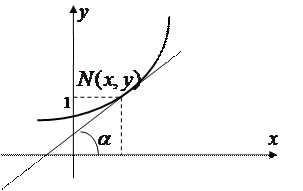Рис.1.
Ответ: .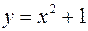
Список литературы
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. тт.I и II, М: Наука, 1985.
2. Письменный Д. Курс лекций по высшей математике. 1 и 2 часть, М: Айрис-пресс, 2005.
3. Ефимов А.В., Демидович Б.П. Сборник задач по математике для втузов, ч.1 и 2, М: Наука, 1993.
4. Данко П.Е. и др.Высшая математика в упражнениях и задачах. М: Высшая школа, 1999.