Линейные ДУ высших порядков с постоянными коэффициентами.

9. Найти общее решение ДУ: .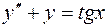

Для решения данного неоднородного ДУ второго порядка применим метод вариации произвольных постоянных (см. лекцию).

Составим характеристическое уравнение 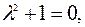найдем его корни 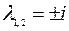(характеристические числа).

Тогда общее решение соответствующего однородного ДУ будет иметь вид:

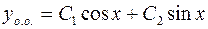, где 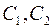– произвольные постоянные.

Будем искать общее решение неоднородного ДУ в ви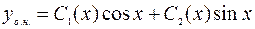де:

, где 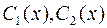– неизвестные функции.

Составим систему:

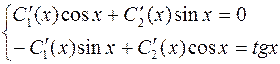(см. лекцию).

Находим из полученной системы (например, методом Крамера):

.

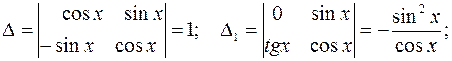
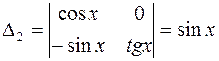Тогда,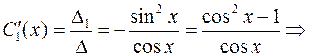

;

.

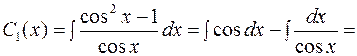
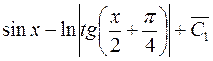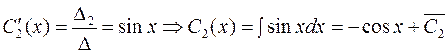Отсюда общее решение неоднородного ДУ будет иметь вид:

= .

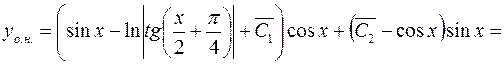
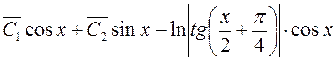Переобозначим произвольные постоянные.

Ответ: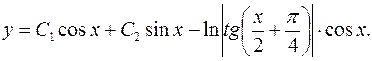

10. Найти частное решение, удовлетворяющее заданному начальному условию (решить задачу Коши): , .

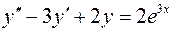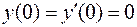Решение.