
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Динамическое торможение. Динамическое торможение в настоящее время является наиболее универсальным способом торможения, поэтому находит широкое применение
|
|
Динамическое торможение в настоящее время является наиболее универсальным способом торможения, поэтому находит широкое применение. При реализации этого способа торможения 3-х фазную статорную обмотку отключают от 3-х фазного источника переменного напряжения и 2-х фазы обмотки статора подключают к источнику постоянного напряжения. В результате в обмотке статора формируется статическое магнитное поле, при взаимодействии которого с вращающимся ротором возникает электромагнитный момент. Этот момент, в соответствии с принципом Ленца, направлен противоположно направлению вращения и является тормозным. Рабочая точка характеристики переходит во 2-ой квадрант, где под действием отрицательного момента двигатель останавливается. Остановка происходит при нулевом моменте ( ,
, 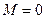 ). Главное отличительное качество динамического торможения - точность.
). Главное отличительное качество динамического торможения - точность.
Интенсивность процесса динамического торможения зависит от величины приложенного постоянного напряжения и от величины добавочного сопротивления, включаемого в цепь статора (для предотвращения перегрева двигателя, т.е. для ограничения тока).
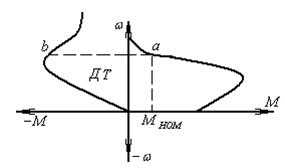
Рис.56 Механическая характеристика АД при динамическом торможении
Так как момент изменяет своё направление, а угловая скорость нет, то произведение момента и угловой скорости отрицательно, следовательно, поток механической энергии направлен от механизма к двигателю, т.е. в паре «двигатель-механизм» (со стороны механизма), режим динамического торможения является генераторным.
При этом вся преобразованная энергия рассеивается в двигателе. Энергия постоянного напряжения идёт на создание статического магнитного потока.
2.5.4 Моделирование ЭП с АД. Асинхронный двигатель, как объект управления. Динамическая модель АД в переменных «входы - выходы»
Математическая модель АД должна представлять собой систему уравнений, описывающих все физические процессы, происходящие в АД (электромагнитные и механические).
Модель в переменных «входы- выходы» будем представлять для одной фазы двигателя. Простейшим инструментом для составления системы уравнений, описывающих электромагнитные процессы АД, является электрическая схема замещения. Наиболее удобна Т-образная приведенная схема замещения АД с учётом механической нагрузки на валу двигателя.
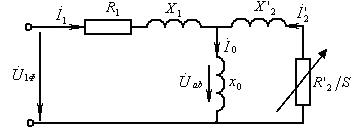
Рис.57 Приведенная Т-образная схема замещения АД с учётом механической нагрузки на валу двигателя
Запишем уравнения для данной схемы.
Уравнения контуров:
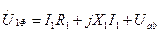 , (37)
, (37)
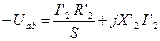 (38)
(38)
Уравнение электрического равновесия ветви намагничивания:
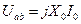 (39)
(39)
Уравнение движения:
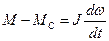 . (40)
. (40)
Уравнение по 1-му закону Кирхгофа:
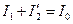 . (41)
. (41)
Уравнение момента:
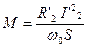 . (42)
. (42)
Скольжение:
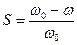 . (43)
. (43)
Заменим в уравнениях (37)-(39) 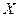 на
на 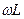 .
.
Запишем уравнения (37)-(39) и (43) в операторной форме.
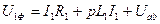 (44)
(44)
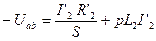 (45)
(45)
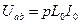 (46)
(46)
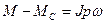 (47)
(47)
Для того, чтобы представить динамическую модель в переменных «входы-выходы» необходимо:
1) выбрать входные и выходные переменные;
2) решить каждые из уравнений (41) - (47) относительно одной из переменных и представить графический образ каждого уравнения;
3) объединить графические образы семи уравнений в один, в соответствии с поставленной задачей, получив структурную схему модели в переменных «входы-выходы».
Итак, представим графический образ уравнения (41).
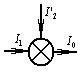
Рис.58а Динамическая модель
Схема, соответствующая уравнению (42), представлена на рис.58б.
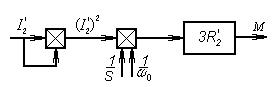
Рис.58б Динамическая модель
Преобразуем уравнение (43) и представим его графический образ.
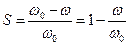
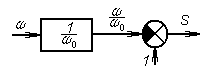
Рис.58в Динамическая модель
Решим уравнение (44) относительно 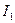 :
:
 .
.
Введем коэффициент пропорции 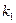 и постоянную времени
и постоянную времени  :
:
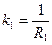 ,
,
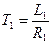 .
.
Тогда уравнение примет вид:
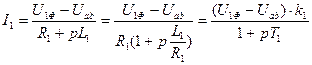 .
.
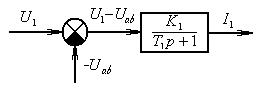
Рис.58г Динамическая модель
Решим уравнение (45) относительно 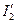 :
:
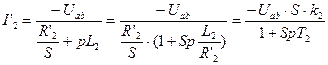 ,
,
где 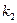 - коэффициент пропорции,
- коэффициент пропорции,
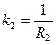 ;
;
 - постоянная времени,
- постоянная времени,
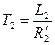 .
.
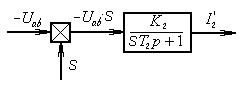
Рис.58д Динамическая модель
Схема, соответствующая уравнению (46), представлена на рис.58е.
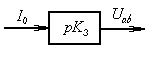
Рис.58е Динамическая модель
Графический образ, соответствующий уравнению (47), показан на рис.58ж.

Рис.58ж Динамическая модель
Для построения общей структурной схемы объединим полученные выше графические образы.
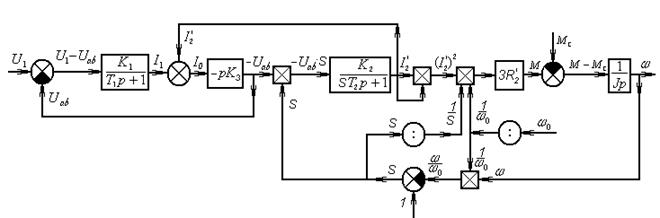
Рис.58з Динамическая модель АД в переменных «входы-выходы»