Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение механических характеристик с использованием формулы Клосса
|
|
Выражение зависимости вращающегося электромагнитного момента от скольжения 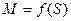 - формула Клосса. Ее получают путем деления
- формула Клосса. Ее получают путем деления 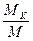 .
.
После проведения несложных алгебраических операций получим выражение, формулу Клосса:
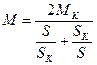 (33)
(33)
Перегрузочная способность двигателя:
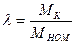
Если в уравнение (28) вместо момента 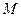 подставить
подставить 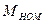 , получим:
, получим:
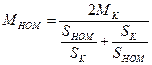 (34)
(34)
Решим (34) относительно критического скольжения 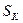 :
:
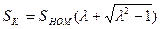 (35)
(35)
Используя эти выражения, а, также зная паспортные данные двигателя, легко можно построить механические характеристики 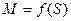 ,
,  .
.
Последовательность промежуточных расчетов приведена в курсе «ЭП». Построение характеристик сводится к использованию уравнений (33) и (29):
В интервале от 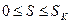 выбираем шаг не более 0, 01, т.е.
выбираем шаг не более 0, 01, т.е. 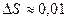 .
.
В интервале от 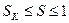 шаг
шаг 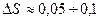 .
.
Получим характеристики аналогичные построенным ранее.

Рис.46 Механическая характеристика АД - 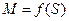
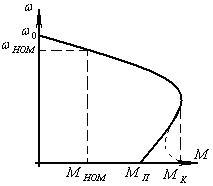
Рис.47 Механическая характеристика АД - 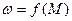
Эти характеристики, отличаются от экспериментальных механических характеристик тем, что реальный пусковой момент 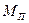 несколько больше, чем расчётный, при скольжении
несколько больше, чем расчётный, при скольжении 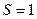 .
.
Реальные механические характеристики имеют некоторый провал в области скольжения 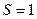 . Это связанно с тем, что в расчётных характеристиках построенных с помощью формулы Клосса не учитываются конструктивные особенности двигателя, направленные на улучшение их пусковых свойств (двигатель с глубоким пазом или с роторной обмоткой типа беличьего колеса). Части характеристик, описывающих устойчивую работу (рабочие части характеристик) при скольжении
. Это связанно с тем, что в расчётных характеристиках построенных с помощью формулы Клосса не учитываются конструктивные особенности двигателя, направленные на улучшение их пусковых свойств (двигатель с глубоким пазом или с роторной обмоткой типа беличьего колеса). Части характеристик, описывающих устойчивую работу (рабочие части характеристик) при скольжении 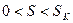 практически точно совпадают.
практически точно совпадают.
Построение искусственных механических характеристик с использованием формулы Клосса несколько затруднительно в связи с тем, что для этого требуется уравнения зависимостей:
а) 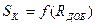 ;
;
б) 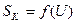 ;
;
в) 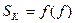 .
.
Достаточно точно эта зависимость может быть определена только для случая (а).
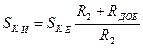 ,
,