
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Локальная теорема Лапласа
|
|
Формула Бернулли позволяет вычислить вероятность того, что событие появиться в n испытаниях ровно k раз: P  (k) =
(k) = 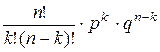
При применении формулы учитывается, что вероятность появления события в каждом испытании постоянна. Легко видеть, что пользоваться формулой Бернулли при больших значениях n достаточно трудно.
Естественно, возникает вопрос: нельзя ли вычислить интересующую нас вероятность, если число испытаний велико, не прибегая к формуле Бернулли? Оказывается, можно.
Локальная теорема Лапласа и дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно k раз в n испытаниях, если число испытаний достаточно велико.
Локальная теорема Лапласа.
Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р  (k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n):
(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n):
Р  (k) =
(k) = 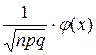
где 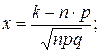 φ (x) =
φ (x) = 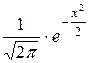 ; q = 1 – p.
; q = 1 – p.
Имеются таблицы, в которых помещены значения функции φ (x)= 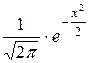 ,
,
соответствующие положительным значениям аргумента x (см. приложение 1).
Для отрицательных значений аргумента пользуются теми же таблицами, так как φ (х) – функция четная, то есть φ (–x) = φ (x).
Пример. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании
равна 0, 2.
Решение. По условию, n=400; k=80; p=0, 2; q=0, 8.
Воспользуемся формулой Лапласа:
Р 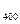 (80)≈
(80)≈ 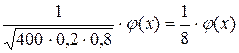 .
.
Вычислим определяемое данными задачи значение х:
x = (k–np) / 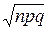 = (80 – 400 ∙ 0, 2) / 8 = 0
= (80 – 400 ∙ 0, 2) / 8 = 0
По таблице приложения 1 находим φ (0)=0, 3989.
Искомая вероятность:
Р 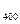 (80)= (1/8)∙ 0, 3989=0, 04986.
(80)= (1/8)∙ 0, 3989=0, 04986.
Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости опущены): Р  (80)=0, 0498.
(80)=0, 0498.