Интегральная теорема Лапласа

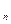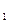Вновь предположим, что производится n испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0< p< 1). Как вычислить вероятность P (k , k 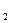) того, что событие А появится в n испытаниях не менее k 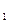и не более k 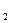раз (для краткости будем говорить «от 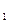k до k 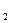раз»)? На этот вопрос отвечает интегральная теорема Лапласа, которую мы приводим ниже.

Интегральная теорема Лапласа.

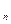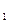Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P (k , k 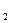) того, что событие А появится в n испытаниях от 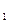k до k 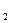раз, приближенно равна определенному интегралу:

,

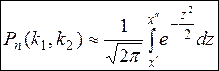где 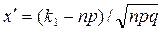и .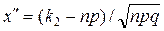

При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл 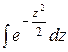, не выражается через элементарные функции. Таблица для функции Φ (х) = 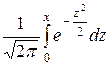приведена в приложении 2. В таблице даны значения функции Ф(х) для неотрицательных значений х; для х< 0 пользуются той же таблицей, так как Ф(х) – функция нечетная: Ф(–х) = – Ф(х). В таблице приведены значения функции лишь до х = 5, так как для x> 5 можно принять Ф(х) = 0, 5. Функцию Ф(х) часто называют функцией Лапласа.

Пример. Вероятность того, что деталь не прошла проверку ОТК, равна 0, 2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100.

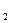Решение. По условию р = 0, 2; q=0, 8; n= 400; k =70; k =100.

Вычислим верхний и нижний пределы интегрирования:

.

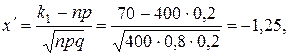
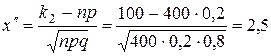Таким образом, получаем:

P 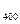(70; 100) = Ф (2, 5) – Ф(–1, 25) = Ф (2, 5) + Ф(1, 25),

так как Ф(–1, 25) = –Ф (1, 25).

По таблице приложения 2 находим:

Φ (2, 5) = 0, 4938, Φ (1, 25) = 0, 3944.

Искомая вероятность: P 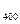(70; 100) = 0, 4938 + 0, 3944 = 0, 8882.