
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формула Пуассона
|
|
Пусть производится n независимых испытаний¸ в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений события в испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической локальной формулой Лапласа. Однако, эта формула непригодна, если вероятность события мала (р ≤ 0, 1). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона.
Итак, поставим перед собой задачу найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз. Сделаем важное дополнение: произведение n∙ p сохраняет постоянное значение, а именно, n∙ p=λ.
Формула Пуассона имеет вид:
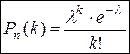 ,
,
где λ =n∙ p.
Эта формула выражает закон Пуассона распределения вероятностей массовых (n велико) и редких (р мало) событий.
Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредиться равно 0, 0002. Найти вероятность того, что на базу прибудут три негодных изделия.
Решение. По условию n=5000; р = 0, 0002; k = 3. Найдем λ:
λ = n ∙ p= 5000 ∙ 0, 0002 = 1.
Искомая вероятность по формуле Пуассона равна:
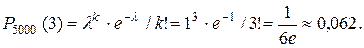
§9. Дискретные случайные величины.
Закон распределения дискретной случайной величины
Определение. Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа, которые эта величина принимает с определенными вероятностями.
То есть, возможные значения дискретной случайной величины можно перенумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счетным).
Определение. Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей.
Закон распределения дискретной случайной величины Х может быть задан в виде таблицы, первая строка которой возможные значения xi, а вторая–вероятности pi.
| Х | x1 | x2 | … | xn |
| p | p1 | p2 | … | pn |
В случае, когда множество значений дискретной случайной величины конечно, сумма вероятностей равна единице:
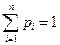 .
.
Если множество возможных значений случайной величины х бесконечно (счетно), то закон распределения будет иметь следующий вид:
| Х | x1 | x2 | … | xn | … |
| P | p1 | p2 | … | pn | … |
где ряд 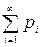 сходится и его сумма равна единице:
сходится и его сумма равна единице:
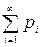 =1.
=1.
Закон распределения дискретной случайной величины х может быть также задан аналитически
P(Х = 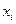 ) = j(
) = j(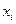 )
)
или с помощью функции распределения.
Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки M1(x1; p1), M2(x2; p2), …, Mn(xn; pn) (xi – возможные значения, pi – соответствующие вероятности) и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
Пример 1. Дискретная случайная величина Х задана законом распределения:
| Х | ||||
| Р | 0, 2 | 0, 1 | 0, 4 | 0, 3 |
Построить многоугольник распределения.
Решение. Построим прямоугольную систему координат, причем по оси абсцисс будем откладывать возможные значения xi, а по оси ординат–соответствующие вероятности pi.
Построим точки M1(1; 0, 2), M2(3; 0, 1), M3(6; 0, 4) и M4(8; 0, 3). Соединив эти точки отрезками, получим искомый многоугольник распределения.
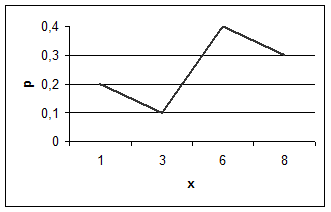
Рис.1 Многоугольник распределения.
Пример 2. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в первом опыте равна 0, 1. составить закон распределения числа отказавших элементов в первом опыте.
Решение. Дискретная случайная величина Х (число отказавших элементов в первом опыте) имеет следующие возможные значения: 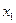 = 0 (ни один из элементов устройства не отказал),
= 0 (ни один из элементов устройства не отказал), 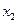 = 1 (отказал один элемент),
= 1 (отказал один элемент), 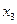 = 2 (отказали два элемента),
= 2 (отказали два элемента), 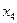 = 3 (отказали три элемента).
= 3 (отказали три элемента).
Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что по условию n = 3, p = 0, 1 (следовательно, q = 1 – 0, 1 = 0, 9), получим:
P3(0) = q³ = 0, 9³ = 0, 729;
P3(1) = C 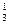 ∙ p¹ ∙ q³ = 3 ∙ 0, 1 ∙ 0, 9³ = 0, 243;
∙ p¹ ∙ q³ = 3 ∙ 0, 1 ∙ 0, 9³ = 0, 243;
P3(2) = С 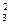 ∙ р² ∙ q¹ = 3 ∙ 0, 1² ∙ 0, 9 = 0, 027;
∙ р² ∙ q¹ = 3 ∙ 0, 1² ∙ 0, 9 = 0, 027;
P3(3) = p³ = 0, 1³ = 0, 001.
Контроль: 0, 729 + 0, 243 + 0, 027 + 0, 001 = 1.
Получаем закон распределения:
| Х | ||||
| Р | 0.729 | 0, 243; | 0, 027 | 0.001 |