
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоремы сложения и умножения вероятностей
|
|
Определение. Суммой А + В двух событий А и В называют событие, состоящее в появлении события А или события В, или обоих этих событий.
В частности, если события А и В несовместные, то А + В – событие, состоящее в появлении только одного из этих событий.
Определение. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.
Теорема сложения вероятностей несовместных событий.
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий.
Р(А + В) = Р(А) + Р(В).
Следствие: вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий.
Р(А 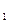 +А
+А 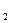 +…+А
+…+А 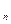 ) = Р(А
) = Р(А 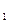 ) + Р(А
) + Р(А 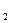 ) + … + Р(А
) + … + Р(А 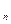 )
)
Пример. В ящике 15 деталей, среди которых 5 окрашенных. Сборщик наудачу достает 3 детали. Найти вероятность того, что из трех взятых деталей окрашенной окажется хотя бы одна деталь.
Решение. Требование – хотя бы одна из трёх деталей окрашена – будет осуществлено, если произойдет любое из следующих 3 несовместных событий: В – одна деталь из трех окрашена, С – две детали из трех окрашены, D – три детали окрашены. Интересующее нас событие А можно представить в виде суммы событий: А = В + С + D, и по теореме о вероятности суммы несовместных событий получаем
Р(А) = Р(В) + Р(С) + Р(D).
Р(B) = 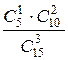 =
= 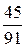 = 0, 495;
= 0, 495;
Р(С) = 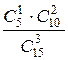 =
= 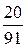 = 0, 220;
= 0, 220;
Р(D) = 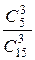 =
= 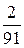 = 0, 022;
= 0, 022;
тогда Р(А) = Р(В) + Р(С) + Р(D) = 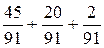 =
= 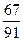 = 0, 736.
= 0, 736.
(Если сложить числа 0, 495, 0, 220 и 0, 022, то получится 0, 737, что не равно 0, 736. Погрешность получается в результате округлений.)
Определение. Два события А и В называются независимыми, есливероятность появления одного из них не меняется от появления или непоявления другого и наоборот.
Пример. Рассмотрим две урны с шарами. В каждой урне по 5 красных и 6 синих шаров. Из каждой урны один за другим вынимаются два шара, но в первой урне шары возвращаются (урна с возвратом), а во второй урне не возвращаются (урна без возврата). Рассмотрим событие А – второй вынутый из урн шар красный. В первом случае (с возвратом) вероятность события А не зависит от того каким был вынут первый шар (красный или синий), а во второй урне (без возврата) вероятность события А зависит от того, какой был вынут первый шар (красный или синий).
Условную вероятность появления события В при условии, что произошло событие А обозначим символом:
Р 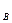 (А) или P(A/B).
(А) или P(A/B).
Определение. Произведением двух событий А и В называют событие А∙ В, состоящее в совместном появлении этих событий. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.
Теорема умножения вероятностей независимых событий:
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий
Р(А ∙ В) = Р(А) · Р(В)
Теорема умножения вероятностей зависимых событий
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило:
Р(А ∙ В) = Р(А) · Р 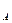 (В) = Р(В) ∙ Р
(В) = Р(В) ∙ Р 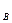 (А)
(А)
Теорема сложения вероятностей совместных событий
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
Р(А + В) = Р(А) + Р(В) – Р(А ∙ В).
Теорема может быть обобщена на любое конечное число совместных событий.
