Частные производные высших порядков

Пусть функция 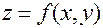имеет в области 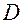частные производные 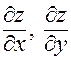. Функции 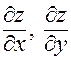в свою очередь могут иметь частные производные в области 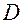или более узкой области. Эти частные производные называются частными производными второго порядка исходной функции .

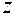У функции двух переменных могут быть четыре разных частных производных второго порядка:

1) 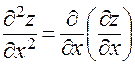, или в других обозначениях ;

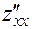2) 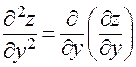, или в других обозначениях ;

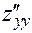3) 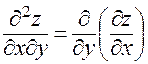, или в других обозначениях ;

4) 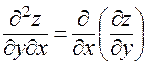, или в других обозначениях .

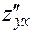Исходные частные производные 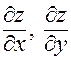называются при этом частными производными первого порядка.

Аналогично определяются и частные производные более высоких порядков от функций двух и более переменных.

Пример. У функции 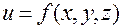среди частных производных третьего порядка имеются в том числе следующие:

; ; .

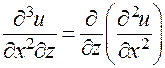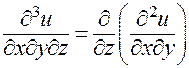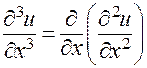и т. д.

Те из частных производных второго и более высоких порядков, у которых дифференцирование ведется по различным переменным, называются смешанными. Так, в последнем примере первые две из частных производных третьего порядка являются смешанными.

Пример. Рассмотрим функцию 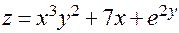. Здесь

; .

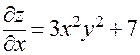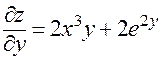Далее,

; ; ;

.

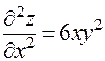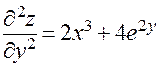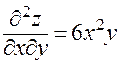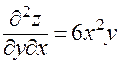Совпадение смешанных частных производных 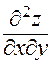и 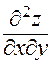в последнем примере является неслучайным; именно справедлива следующая

Теорема. Пусть выполнены два условия:

1. В окрестности точки 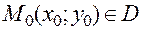существуют частные производные 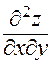и .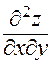

2. В самой точке 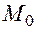смешанные частные производные 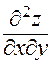и 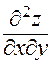непрерывны.

Тогда имеет место равенство смешанных частных производных:

.

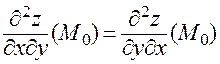(без доказательства).