Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
II. Понятие производной по направлению
|
|
Пусть в области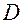 
плоскости 
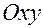заданы функция двух переменных 
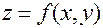, точка 
, и ненулевой вектор 
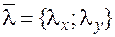. Будем выбирать переменную точку 
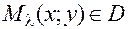таким образом, чтобы вектор 
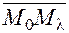был сонаправлен с вектором 
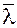(рис. 21).
Обозначим приращения независимых переменных при переходе от точки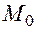 
к точке 
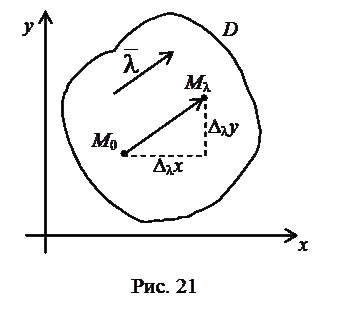
через 
, 
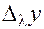; соответст
 |
вующее приращение функции через
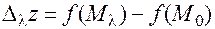. Тогда
.
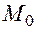Определение. Пусть стремится к точке таким образом, что вектор 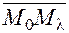остается направленным одинаково с вектором 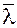. Если существует конечный предел отношения 
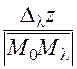при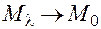 
, то этот предел называется производной функции 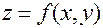по направлению вектора 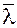в точке .
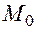Обозначение производной по направлению: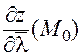 
. Итак, согласно определению:
.
Замечание. Производная по направлению показывает скорость изменения функции в точке 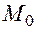в направлении вектора 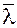. В частности производные по направлению базисных ортов равны соответствующим частным производным:
.
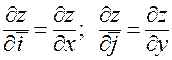Пусть вектор 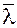имеет направляющие косинусы 
, 
.
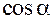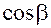Теорема. Пусть функция 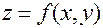удовлетворяет двум условиям:
1. В окрестности точки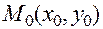 
она имеет частные производные 
.
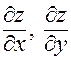2. В самой точке 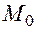частные производные непрерывны.
Тогда для производной по направлению 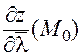справедлива формула:
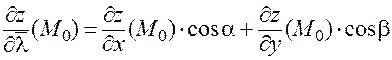. (24)
Доказательство. Пусть , 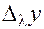— приращения независимых переменных, соответствующие переходу от точки 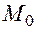к точке . Ввиду непрерывности частных производных для соответствующего приращения функции 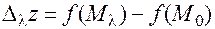справедлива формула:
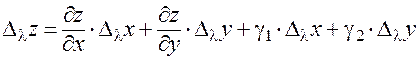, (25)
где функци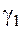и 
и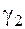 
― бесконечные малые величины пр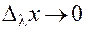и 
и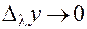 
(п. 6). Деля обе части (25) на 
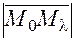, получаем:
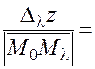
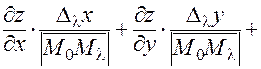
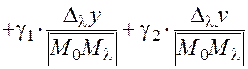. (26)
Поскольку вектор 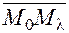сонаправлен с вектором 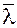, то величина 
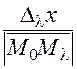, будучи направляющим косинусом вектора 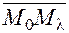, совпадает с направляющим косинусом вектора : 
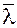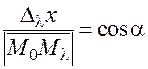. Аналогично 
.
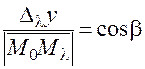Равенство (26) теперь принимает вид:
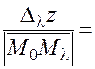
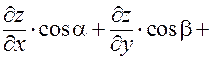
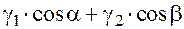. (27)
Поскольку , , 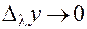когда 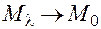, то переходя в (27) к пределу при 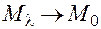, получаем на основании свойств предела:
. ▄
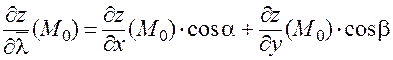Пример. Пусть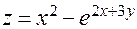 
, 
, 
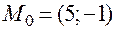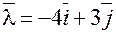. Вычислим производную по направлению 
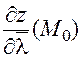. Находим частные производные:
; 
;
; 
.
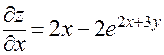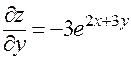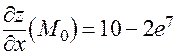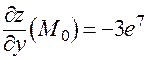Находим направляющие косинусы вектора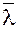 
:
; 
.
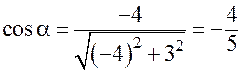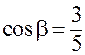Подставляем найденные значения в формулу (24):
.
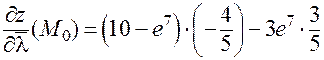Аналогичным образом определяется производная по направлению в случае функции трех или более переменных. Для функции трех переменных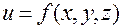 
формула (24) (в случае непрерывности частных производных) принимает вид:
.
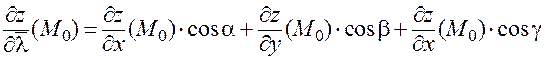